Identifying Complex Splitting
Key Questions
-
The coupling constant
#J# is pretty much the peak-to-peak distance, usually reported in#"Hz"# . Matching it up with other nearly-identical coupling constants elsewhere in the spectrum usually tells you which protons are near which others.
For example:
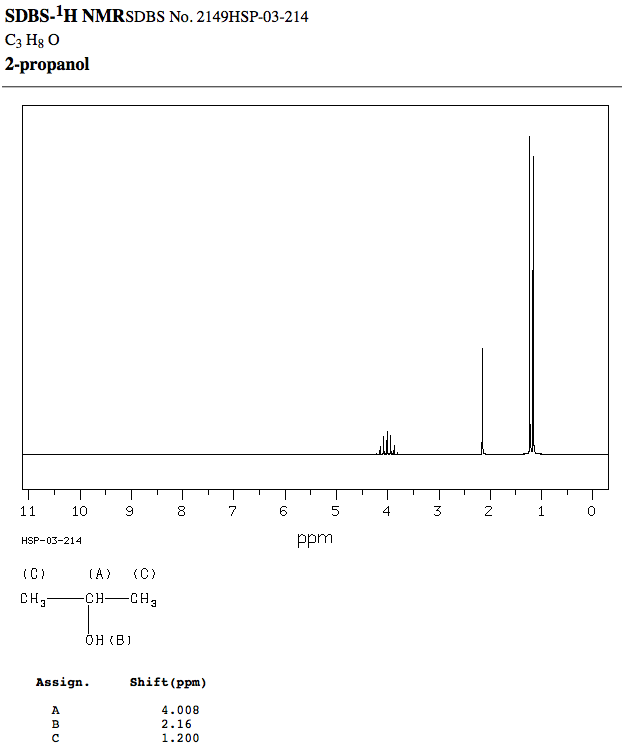
Peak Data:
#"Hz"" "" " "" " ppm"" ""Intensity"# Proton A:
#"371.56"" ""4.149"" ""24"#
#"365.38"" ""4.080"" ""56"#
#"359.25"" ""4.012"" ""72"#
#"353.13"" ""3.943"" ""60"#
#"347.06"" ""3.876"" ""28"# Proton B:
#"193.00"" ""2.155"" ""335"# Proton C:
#"110.44"" ""1.234"" ""1000"#
#"108.19"" ""1.209"" ""27"#
#"104.31"" ""1.165"" ""939"#
#"102.06"" ""1.140"" ""25"# What is shown here for proton A is that
#"4.008 ppm"# is the average chemical shift of the 1-4-6-4-1 pattern (according to Pascal's triangle) from the rightmost peak to the leftmost peak, and the entire signal there has multiple peaks. The peaks split like so:1
#-># 1-1#-># 1-2-1#-># 1-3-3-1#-># 1-4-6-4-1It is not visible in this zoom, but the distance between each peak is roughly identical. This distance is the numerical equivalent of the coupling constant
#J# in#"Hz"# . For proton A:#4.149 - 4.080 = "0.069 ppm"#
#4.080 - 4.012 = "0.068 ppm"#
#4.012 - 3.943 = "0.069 ppm"#
#3.943 - 3.876 = "0.067 ppm"# Interestingly enough, if you look at protons C at the averaged
#"1.200 ppm"# , you would also see that that doublet has the same#J# value (ideally that doublet should have both peaks at identical intensities too, but the shimming was not perfect, so they are a bit off). For proton C:#1.234 - 1.165 = "0.068 ppm"# From the identical (or nearly-identical) coupling constant, you can determine which protons are "communicating" with each other and thus which protons they neighbor.
If you take this number and multiply it by the
#"MHz"# of your NMR, you get the coupling constant in#"Hz"# . So, if your NMR's magnetic field frequency is#"89.56 MHz"# (like for this particular spectrum), then:#"0.068 ppm" * "89.56 MHz"# # = 0.068 ("Hz")/("MHz") * "89.56 MHz"# #= color(blue)"6.09 Hz"# Indeed, for proton C,
#110.44 - 104.31 = "6.13 Hz" ~~ "6.09 Hz"# .Therefore, without seeing the structure of the analyzed molecule, you can still figure out that proton A and protons C are coupling/"communicating" with each other.
-
Answer:
NMR provides information on how many hydrogen neighbors exist for a particular hydrogen or group of equivalent hydrogens. In general, an NMR resonance will be split into N + 1 peaks where N = number of hydrogens on the adjacent atom or atoms.
Explanation:
If there are no hydrogens on the adjacent atoms, then the resonance will remain a single peak, a singlet.
If there is one hydrogen on the adjacent atoms, the resonance will be split into two peaks of equal size, a doublet.
Two hydrogens on the adjacent atoms will split the resonance into three peaks with an area in the ratio of 1:2:1, a triplet.
If there are 3 hydrogens on the adjacent atoms, the resonance will be split into four peaks with an area in the ratio of 1:3:3:1, a quartet. -
To find the NMR splitting pattern, for a given hydrogen atom, count how many identical hydrogen atoms are adjacent, and then add one to that number. For example, in
#CH_2ClCH_3# below, the red hydrogen atoms are adjacent to three identical hydrogen atoms (marked in blue). They will exhibit a quartet (4 peak; 3+1) splitting pattern. For the blue hydrogens, they are adjacent to two identical hydrogen atoms (marked in red), so their splitting pattern will be a triplet.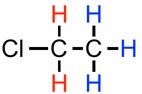
To illustrate this concept with one more example, with propane,
#CH_3CH_2CH_3# . Each of the blue hydrogen atoms are still adjacent only to two identical hydrogen atoms, so they will still exhibit a triplet splitting pattern (2+1). This time, however, the red hydrogens are adjacent to six identical hydrogen atoms (with a symmetrical molecule such as propane, all the the blue hydrogen atoms are chemically identical). The resulting splitting pattern will be a seven-peaked septet (6+1).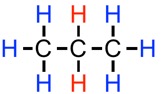
The physics behind NMR splitting has already been explained in an earlier post.
Sometimes things can get tricky when you have molecules where hydrogen atoms are adjacent to two different sets of identical hydrogen atoms. If you are interested in this more complex situation, please post in the comments.