What are the extrema and saddle points of #f(x, y) = 6 sin(-x)* sin^2( y)# on the interval #x,y in[-pi,pi]# ?
1 Answer
Explanation:
We have:
# f(x,y) = 6sin(-x)sin^2(y) #
# \ \ \ \ \ \ \ \ \ \ \ = -6sinxsin^2y #
Step 1 - Find the Partial Derivatives
We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constant. Thus:
The First Derivatives are:
# f_x = -6cosxsin^2y#
# f_y = -6sinx(2sinycosy) #
# \ \ \ = -6sinxsin2y #
The Second Derivatives (quoted) are:
# f_(x x) = 6sinxsin^2y #
# f_(yy) = -6sinx(2cos2y) #
# \ \ \ \ \ = -12sinxcos2y #
The Second Partial Cross-Derivatives are:
# f_(xy) = -6cosxsin2y #
# f_(yx) = -6cosx(2sinycosy) #
# \ \ \ \ = -6cosxsin2y #
Note that the second partial cross derivatives are identical due to the continuity of
Step 2 - Identify Critical Points
A critical point occurs at a simultaneous solution of
# f_x = f_y = 0 iff (partial f) / (partial x) = (partial f) / (partial y) = 0#
i.e, when:
# {: (f_x = -6cosxsin^2y, = 0, ... [A]), (f_y = -6sinxsin2y, = 0, ... [B]) :}}# simultaneously
Consider equation [A]
# -6cosxsin^2y = 0 #
Then we have two solutions:
# cosx = 0 => x = +- pi/2 #
# sin y = 0 => y = 0, +- pi#
Now let us use Eq[B] to find the corresponding coordinate:
# x = +-pi/2 => sin2y = 0 #
# \ \ \ \ \ \ \ \ => 2y = +-pi, +- 2pi => y = +- pi/2, +-pi #
# y=0,+-pi => x in RR # (gutters)
Which gives us the following critical points:
# (+-pi/2, +-pi/2) \ \ \ \ \ \ # (4 critical points)
# (+-pi/2, +-pi) \ \ \ \ \ \ \ \ # (4 critical points)
# (alpha, 0) \ \ \ \ \ \AA alpha in RR \ \ \ # (gutter line)
# (alpha, +-pi) \ AA alpha in RR \ \ # (2 gutter lines)
Consider equation [B]
# -6sinxsin2y = 0 #
Then we have two solutions:
# sinx \ \= 0 => x = 0,+- pi #
# sin2y = 0 => 2y = 0+- pi, +-2pi#
# \ \ \ \ \ \ \ \ => y = 0, +-pi/2, +- pi #
Now let us use Eq[A] to find the corresponding coordinate@
# x=0,+-pi => siny=0 => y=0,+-pi # (repeats of above)
# y=0 => x in RR # (repeat of above)
# y = +-pi/2 => cosx = 0 #
# \ \ \ \ \ \ \ \ => x=+-pi/2 # (repeats of above)
Which gives us no additional critical points:
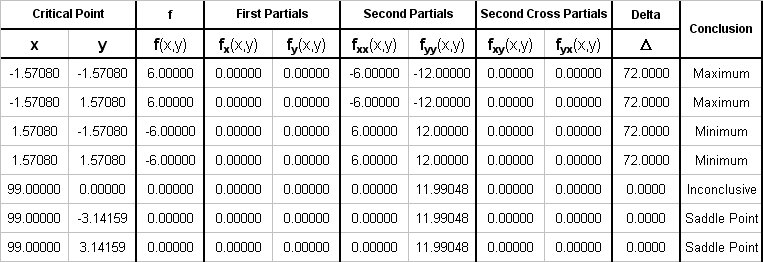
Step 3 - Classify the critical points
In order to classify the critical points we perform a test similar to that of one variable calculus using the second partial derivatives and the Hessian Matrix.
# Delta = H f(x,y) = | ( f_(x x) \ \ f_(xy) ) , (f_(yx) \ \ f_(yy)) | = | ((partial^2 f) / (partial x^2),(partial^2 f) / (partial x partial y)), ((partial^2 f) / (partial y partial x), (partial^2 f) / (partial y^2)) | = f_(x x)f_(yy)-(f_(xy))^2 #
Then depending upon the value of
# {: (Delta>0, "There is maximum if " f_(x x)<0),(, "and a minimum if " f_(x x)>0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :} #
Using custom excel macros the function values along with the partial derivative values are computed as follows:

Here is a plot of the function
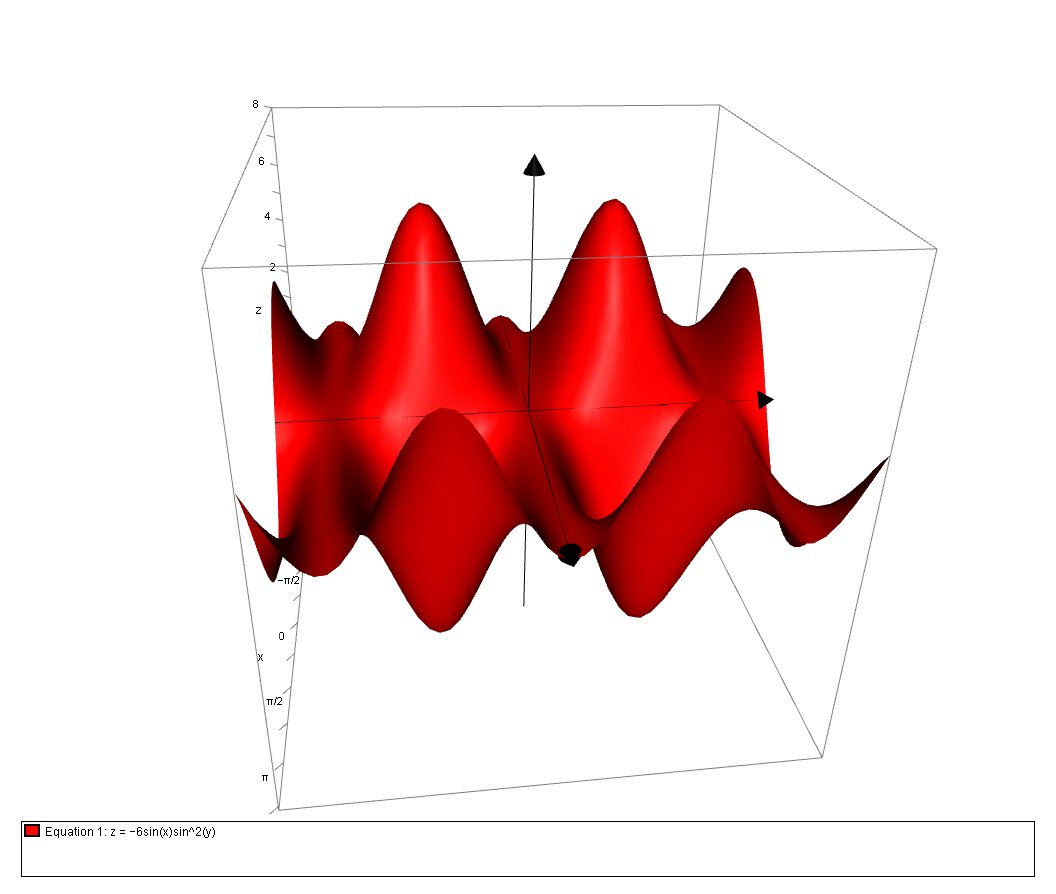
And the ploit with the critical points (and gutters)

