What are the important points needed to graph #y=-x^2+2x+4#?
1 Answer
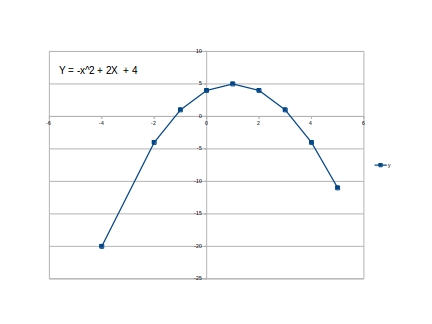
Maybe the easiest one is the x = 0 solution (y = 4). Then, the maximum (in this case), which is the symmetry line of the curve as well.
Explanation:
Because this is a quadratic, we know its shape will be symmetric with a single maximum or minimum.
In this case the curve opens “down” with a maximum point at (1,5).
To sketch the general shape of the curve, the next points to plot would be the solutions for some constant increment of x on either side of the minimum. For example, at x = 2 and x = -2, x = 4 and -4, etc. Plotting (2, 4) (-2, -4) (4, -4) (-4, -20) will give you a general idea of the curve shape.
You can then increase or decrease the increments to get the clarity or smoothness in the curve that you desire. From these initial points the maximum is between the 0 and 2. A few trials identifies the maximum at (1,5).