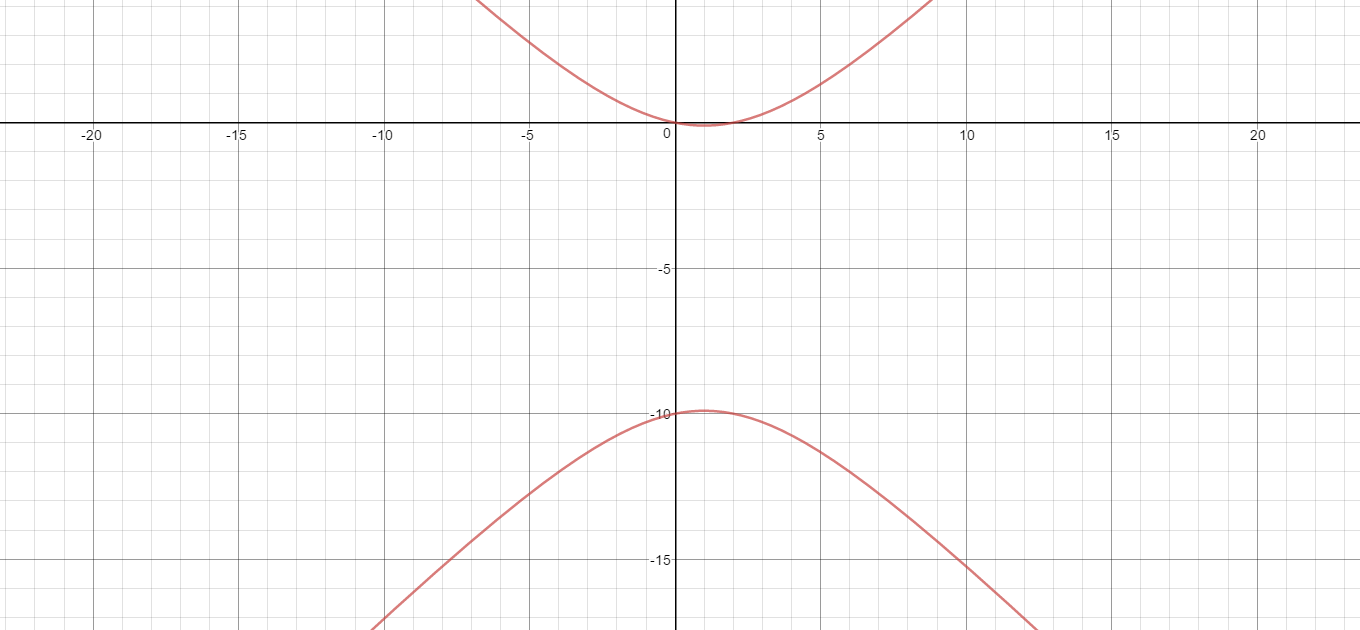
Given: #(x - 1)^2 - (y + 5)^2 = -24#
Here is a graph of the above equation:
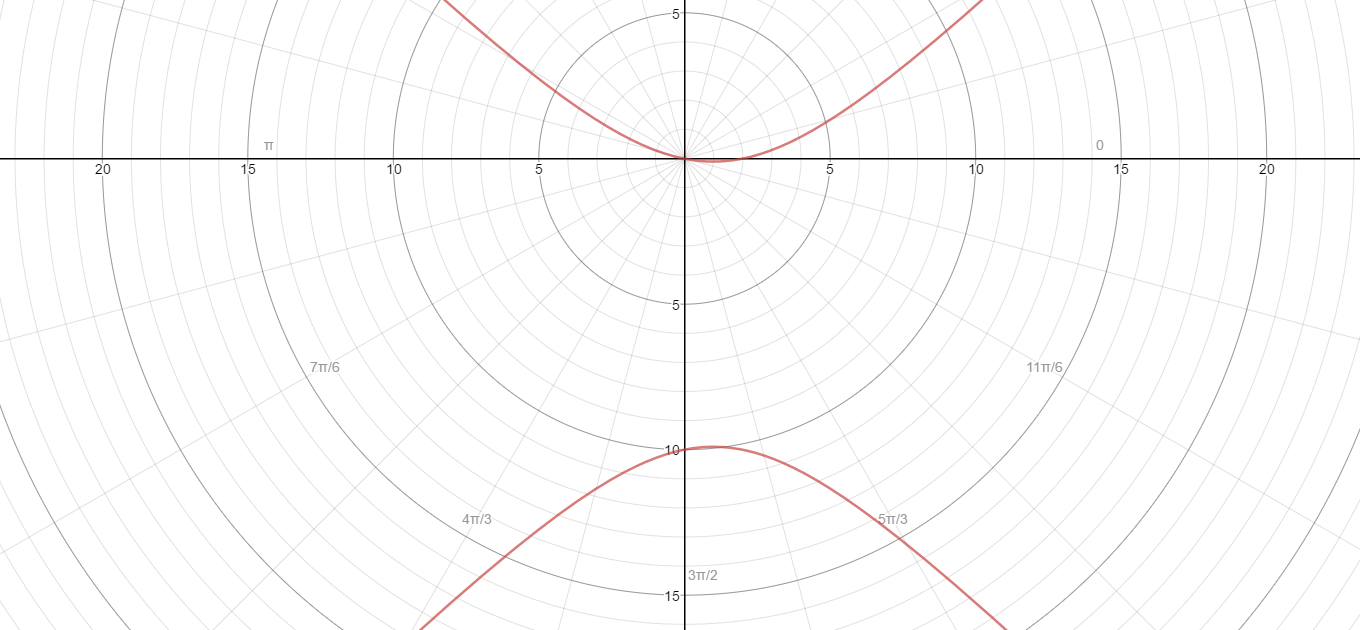
Convert to polar coordinates.
Expand the squares:
#x^2 -2x + 1 - (y^2 + 10y + 25) = -24#
Regroup by power:
#x^2 - y^2 -2x - 10y + 1 - 25 = -24#
Combine the constant terms:
#x^2 - y^2 -2x - 10y = 0#
Substitute #rcos(theta)# for x and #rsin(theta)# for y:
#(rcos(theta))^2 - (rsin(theta))^2 -2(rcos(theta)) - 10(rsin(theta)) = 0#
Lets move the factors of r outside the ():
#(cos^2(theta) - sin^2(theta))r^2 -(2cos(theta) + 10sin(theta))r = 0#
There are two roots, #r = 0# which is trivial should be discarded, and:
#(cos^2(theta) - sin^2(theta))r -(2cos(theta) + 10sin(theta)) = 0#
Solve for r:
#r = (2cos(theta) + 10sin(theta))/(cos^2(theta) - sin^2(theta))#
Here is the graph of the above equation: