Writing Polar Equations for Conic Sections
Key Questions
-
General form of the conic equation
#Ax^2+Bxy+Cy^2+Dx+Ey+F=0# The coefficients
#A# and#C# are need to identify the conic sections without having to complete the square.#A# and#C# cannot be#0# when making this determination.Parabola
#->A*C=0# Circle
#->A=C# Ellipse
#->A*C>0 and A!=C# Hyperbola
#->A*C<0# 
AJ Speller
·
·
Sep 28 2014
-
Standard form equations for the hyperbola.
#x^2/a^2-y^2/b^2=1# The foci are located on the
#x# -axis also called the transverse .#y^2/a^2-x^2/b^2=1# The foci are located on the
#y# -axis also called the transverse .
AJ Speller
·
·
Sep 28 2014
-
Standard form for the equation of a parabola is the same as standard for for a quadratic function:
#y =ax^2+bx+c# Or
#f(x) = ax^2+bx+c# .For graphing, many prefer the vertex form
#y=a (x-h)^2 +k# 
Jim H
·
1
·
Apr 25 2015
-
Answer:
A conic section is a section (or slice) through a cone.
Explanation:
Depending on the angle of the slice, you can create different conic sections,
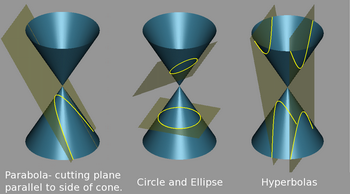
(from en.wikipedia.org)If the slice is parallel to the base of the cone, you get a circle.
If the slice is at an angle to the base of the cone, you get an ellipse.
If the slice is parallel to the side of the cone, you get a parabola.
If the slice intersects both halves of the cone, you get a hyperbola.
There are equations for each of these conic sections, but we will not include them here.
Ernest Z.
·
2
·
Sep 15 2015