Question

What are the possible quantum numbers for the 6d orbital?

Answer 1

Here's what I got.

Explanation:

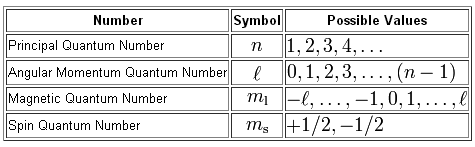
In order for an electron to reside in the d-subshell of any energy level, starting with the third one, it must have a distinct value for its angular momentum quantum number, `l`.

More specifically, the only value of `l` that describes the d-subshell is `l=2`.

In the case of the 6d-subshell, the principal quantum number ,`n`, which gives you the energy level on which the electron can be found, is equal to `6`.

Now, any d-subshell will contain a total of `5` orbitals given by the values of the magnetic quantum number, `m_l`.

For a d-subshell, `m_l` can take the following values

`m_l = {-2; -1; 0; 1; 2}`

Now, the spin quantum number, `m_s`, can only take two possible values

`m_s = -1/2 ->` describes an electron with spin-down
`m_s = +1/2 ->` describes an electron with spin-up

So, to sum this up, the electrons located in the 6d-subshell will have

• `n = 6 ->` the sixth energy level
• `l=2 ->` the d-subshell
• `m_l = { -2; -1; 0; 1; 2} ->` the five d-orbitals found in the d-subshell
• `m_s = +- 1/2 ->` either spin-up or spin-down