What are the products for the alpha decay of #""_64^150Gd#?
1 Answer
Here's what I got.
Explanation:
Alpha decay is said to take place when a radioactive nuclide decays by emission of an
So right from the start, you know that one of the products will be an
#""_(color(white)(x)64)^150"Gd" -> color(blue)(""_x^y?) + ""_2^4"He"#
In order to determine the identity of that
Mass number, which represents the number of protons and neutrons located in the nucleus, is written in the upper-left of the chemical symbol.
The atomic number, which tells you the number of protons located in the nucleus, is written in the lower-left of the chemical element.
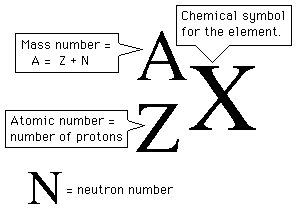
So, looking at your nuclear equation, you can say that
#150 = y + 4 -># conservation of the mass number
and
#64 = x + 2 -># conservation of charge
This will give you
#{(y = 150 - 4 = 146), (x = 64 - 2 = 62) :}#
A quick look in the periodic table will reveal that samarium,
#""_(color(white)(a)64)^150"Gd" -> ""_62^146"Sm" + ""_2^4"He"#

