What are the six trig function values of #-135#?
1 Answer
Mar 17, 2018
As below.
Explanation:

Angle falls in III quadrant where only
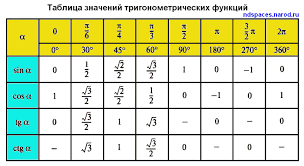
As below.

Angle falls in III quadrant where only
