What determines the probability pattern of an orbital?
1 Answer
It just turned out that way. We can't define equations to influence nature, only describe it.
You can imagine anything you want for what "determines" the probability distribution, but ultimately, nature turned out that way, and we described these orbitals after-the-fact.
DISCLAIMER: This is going to be a long answer.
WHAT IS THE WAVE FUNCTION FOR AN ORBITAL?
Erwin Schrodinger published the wave function
For each orbital, its radial density distribution describes the regions with particular probabilities for finding an electron in that particular orbital.
In general, the wave function for spherical harmonics coordinates can be written as:
#\mathbf(psi_(nlm_l)(r,theta,phi) = R_(nl)(r)Y_(l)^(m_l)(theta,phi))# where:
#r# ,#theta# , and#phi# are spherical coordinates:
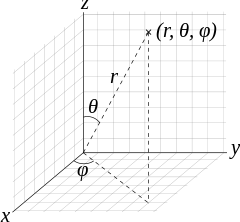
#psi_(nlm_l)# is a wave function that can be constructed to describe what the orbital's electron distribution looks like.It depends on the quantum numbers
#\mathbf(n)# ,#\mathbf(l)# , and#\mathbf(m_l)# .
#R_(nl)# is the radial component of the wave function, describing the variation in the distance from the center of the orbital (the radius!).It depends on the quantum numbers
#\mathbf(n)# and#\mathbf(l)# .
#Y_(l)^(m_l)# is the angular component of the wave function, describing the aspects of the orbital electron distribution that can possibly give it a non-spherical shape.It depends on the quantum numbers
#\mathbf(l)# and#\mathbf(m_l)# .
OKAY, WHAT DOES IT HAVE TO DO WITH PROBABILITY PATTERNS??
Focus on the
When we plot the radial density distribution (or "probability pattern") of an orbital, we plot
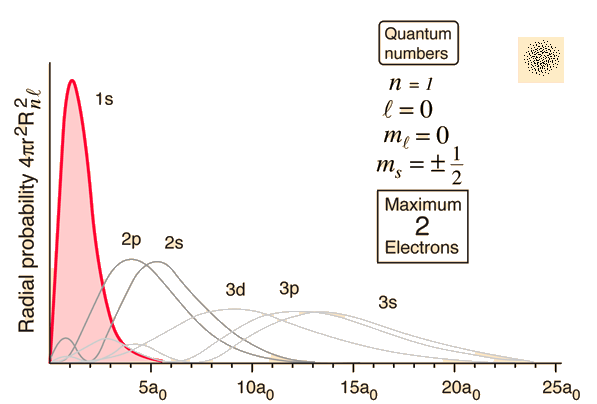
The wave functions themselves, as we defined them, generate these "probability patterns".
HOW DO I KNOW YOU'RE NOT MAKING THIS UP?
Well, with an example, I guess. This will give a result that should prove familiar.
The simplest example of an orbital wave function (used by
#color(blue)(psi_(1s) = R_(10)(r)Y_(0)^(0)(theta,phi)#
#= stackrel(R_(10)(r))overbrace((2Z^"3/2")/(a_0^"3/2")e^(-"Zr/"a_0))*stackrel(Y_(0)^(0)(theta,phi))overbrace(1/sqrt(4pi))#
#= color(blue)(1/sqrt(pi) (Z/(a_0))^"3/2" e^(-"Zr/"a_0))# where:
#Z# is the atomic number of the atom.#a_0# is the same Bohr radius we just defined as#5.29177xx10^(-11) "m"# .
In order to plot the "probability pattern", we have to grab what we need and turn it into
#4pir^2(R_(nl)(r))^2#
#= 4pir^2(stackrel(R_(nl)(r))overbrace((2Z^"3/2")/(a_0^"3/2")e^(-"Zr/"a_0)))^2#
#= 4pir^2(4Z^3)/(a_0^3)e^(-"2Zr/"a_0)#
This is the function that corresponds to the red curve in the diagram above.
Now, since we have the plot for
So...
- Take the derivative with respect to
#r# . - Set it equal to
#0# , since the peak has a slope of#0# .
#=> 16pi(Z/(a_0))^3d/(dr)[r^2e^(-"2Zr/"a_0)]#
Utilize the product rule:
#=> 16pi(Z/(a_0))^3[(-2Z)/(a_0)r^2e^(-"2Zr/"a_0) + 2re^(-"2Zr/"a_0)]#
Now setting it equal to
#0 = cancel(16pi(Z/(a_0))^3)[(-2Z)/(a_0)r^2e^(-"2Zr/"a_0) + 2re^(-"2Zr/"a_0)]#
#0 = (-2Z)/(a_0)r^2e^(-"2Zr/"a_0) + 2re^(-"2Zr/"a_0)#
Although
#0 = ((-2Z)/(a_0)r^2 + 2r)cancel(e^(-"2Zr/"a_0))#
#0 = (-2Z)/(a_0)r^2 + 2r#
#cancel(2)r = (cancel(2)Z)/(a_0)r^2#
#r = (Z)/(a_0)r^2 => color(green)(r = (a_0)/Z)# ...for a Hydrogen-like atom (e.g.
#"He"^(+)# ,#"Li"^(2+)# , etc).
But for the Hydrogen atom,
#\mathbf(color(blue)(r = a_0 = 5.29177xx10^(-11) "m"))# .
That tells us that the electron in the

