What is a 30-60-90 triangle? Please give an example.
1 Answer
A 30-60-90 triangle is a right triangle with angles
Explanation:
A 30-60-90 triangle is a special right triangle, so named for the measure of its angles. Its side lengths may be derived in the following manner.
Begin with an equilateral triangle of side length
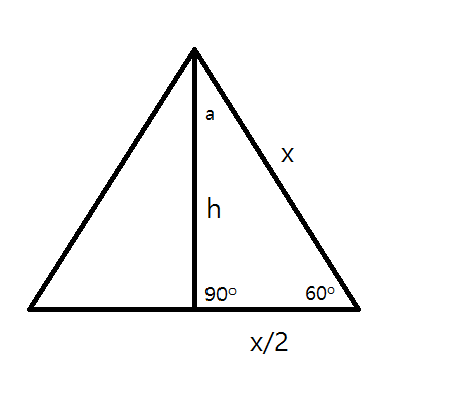
Because the sum of the angles of a triangle is
Furthermore, by the Pythagorean theorem, we know that
Therefore a 30-60-90 triangle with hypotenuse
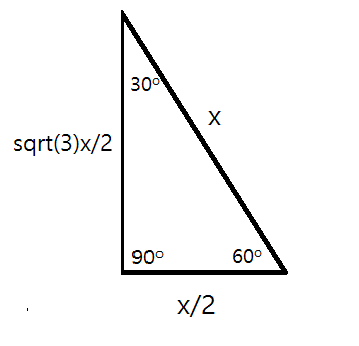
For example, if

