What is a quantum harmonic oscillator?
1 Answer
The quantum harmonic oscillator is essentially a two-body problem consisting of two solid spheres connected by a spring.
A basic version of it is called the simple harmonic oscillator (SHO), in which the spring has no dampening factor (no anharmonicity constant):
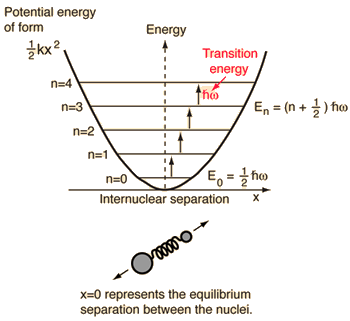
Since there is no dampening factor, the energy levels are evenly spaced, separated by
The Hamiltonian operator for the SHO system in one dimension is:
#color(blue)(hatH_"SHO") = hatK + hatV#
#= -ℏ^2/(2mu)d^2/(dx^2) + 1/2kx^2#
#= [-iℏd/(dx)]^2/(2mu) + 1/2kx^2#
#= color(blue)(hatp^2/(2mu) + 1/2kx^2)# where
#mu = (m_1m_2)/(m_1 + m_2)# is the reduced mass,#hatp# is the momentum operator,#k# is the force constant, and#x# is the relative displacement from equilibrium.#hatK# and#hatV# were the kinetic and potential energy operators.
The normalized wave function for the
#color(blue)(psi_(upsilon)(x) = N_(upsilon)H_(upsilon)(sqrtalphax)e^(-alphax^2"/"2))# where:
#N_(upsilon) = [1/(2^(upsilon) upsilon!)(alpha/(pi))^"1/2"]^"1/2"# is the normalization constant.#H_(upsilon)(sqrtalphax) = (-1)^(upsilon)e^(-alphax^2)d^(upsilon)/(d (sqrtalphax)^(upsilon))[e^(-alphax^2)]# is the Hermite polynomial.#alpha = sqrt((kmu)/(ℏ^2))# is a variable defined for convenience of expressing the function.
Applying the variational method on some trial wave function,
#color(blue)(E_0 = 1/2ℏomega)#
which is in general,
#bb(E_(upsilon) = ℏomega(upsilon + 1/2))# ,
as shown in the first image.