What is ΔE for the transition of an electron from n = 7 to n = 4 in a Bohr hydrogen atom? What is the frequency, v, of the spectral line produced?
1 Answer
Jun 12, 2016
Explanation:
The Bohr Model for the energy of an electron in a hydrogen atom gives us:
Where
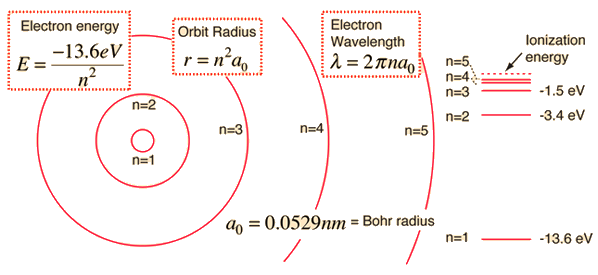
For the transition
To convert this to Joules we multiply by the electronic charge:
To find the frequency of the emitted photon we use the Planck expression:

