What is Ground-state and Excited state of an atom?Thanks..
1 Answer
It is essentially the difference between an atom with extra energy (excited-state) and the same atom in its most stable state, with no extra energy (ground-state).
Let's say we looked at sodium (
#1s^2 2s^2 2p^6 3s^1#
If we shine a light source onto sodium that successfully excites the
The new configuration is:
#1s^2 2s^2 2p^6 3p^1#
Of course, we should recognize that the
HOW TO PREDICT EXCITED STATES?
By what's known as the "selection rules", we can predict possible excitation pathways.
- An electron can only jump up into an orbital that retains the total electron spin (
#DeltaS = 0# ) - We must make sure the total change in angular momentum
#l# is exactly#pm1# (#DeltaL = pm1# ).
Thus, for
For instance:
#3s -> 3p# is allowed.#l# changed by exactly#pm1# .#3s -> 5p# is allowed, if you have enough energy.#3s -> 4s# and#3s -> 5s# are forbidden, because you did not change#l# by#pm1# in one step.#3s -> 3d# is forbidden, because#l# changed by more than#pm1# at a time. However,#3s -> 3p -> 3d# is allowed.#3s -> 3p -> 5s# is allowed, because you changed#l# by#pm1# each time.
Let's put this into a picture.
SODIUM ENERGY LEVEL DIAGRAM
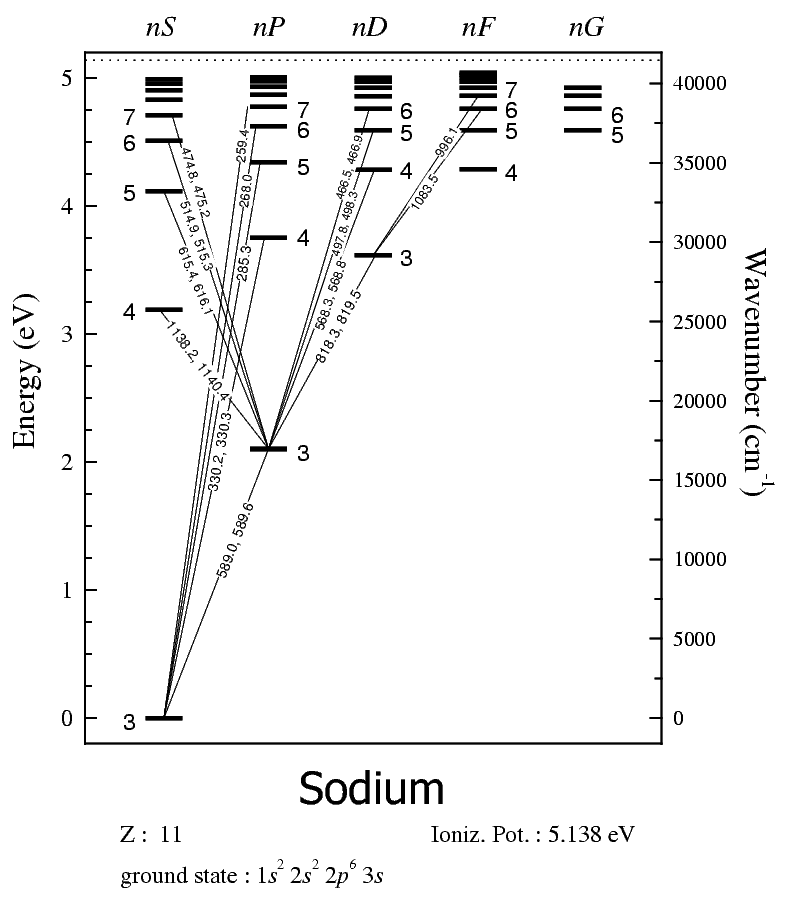
You read this diagram by noting that the
The energy on the left is in
From this diagram, you should realize that the allowed transitions up to new excited states are all diagonal.
Can you trace the excitation pathways from the examples above? You should find that the forbidden transitions are all vertical or require two diagonal steps.

