What is raman spectroscopy?
1 Answer
Raman spectroscopy is IR spectroscopy's more subtle cousin.
It is a light scattering technique that scans for a change in polarizability for a molecule's motions and plots a spectrum for the vibrational motions that may or may not be detectable by IR spectroscopic techniques.
DISCLAIMER: This is going to be difficult, so if you have any questions, feel free to ask. I talk about the concept behind Raman and contrast it with IR. Then I look at more of the technical details behind the technique.
CHANGE IN DIPOLE MOMENT VS CHANGE IN POLARIZABILITY
A change in dipole moment occurs when a molecule's electron distribution is distorted in such a way that the net direction of charge changes. This is especially true for asymmetric stretches and bends.
Building on that, a change in polarizability is the change in the ease at which a molecule's electron cloud can be distorted. It is the change in the change in the dipole moment.
Another way to say it is to let dipole moment be
#(dalpha)/(dQ) = (d^2mu)/(dQ^2)# where
#Q# is#r# (distance) for a stretch or#theta# (angle) for a bend.
When a change in dipole moment is itself asymmetrical, the molecule has IR-active peaks. That is, it gives rise to peaks in the IR spectrum.
Likewise, when a change in polarizability is itself asymmetrical, the molecule has Raman-active peaks. That is, it gives rise to peaks in the Raman spectrum.
HOW DO WE DETERMINE WHETHER A MOTION IS IR OR RAMAN ACTIVE (OR BOTH)?
Let's take carbon dioxide as an example. Being a polyatomic linear molecule, it has
#:stackrel(..)("O")="C"=stackrel(..)("O"):#
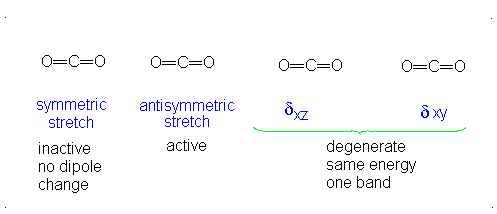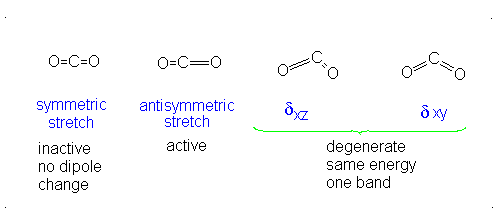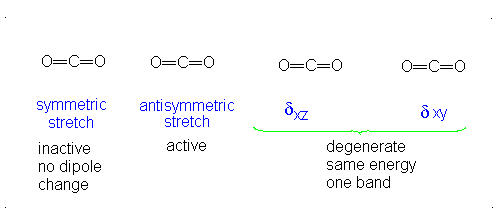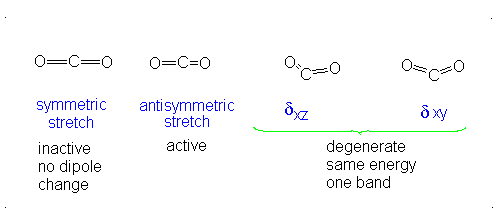
The third vibrational mode is on a plane perpendicular to the plane of the screen/paper. Examining each motion...
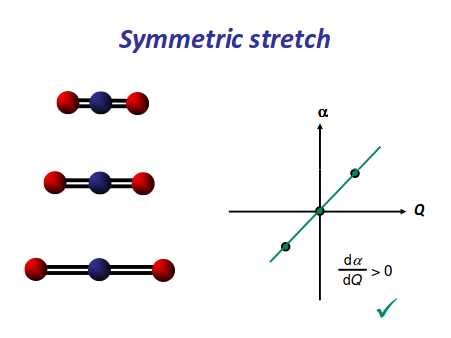
There is neither a change in dipole moment nor generation of an induced dipole because both oxygens move in opposite directions. It is IR inactive. However, as the oxygen atoms move outwards, the molecule becomes easier to polarize, and vice versa, making the graph asymmetrical, so this is Raman active.
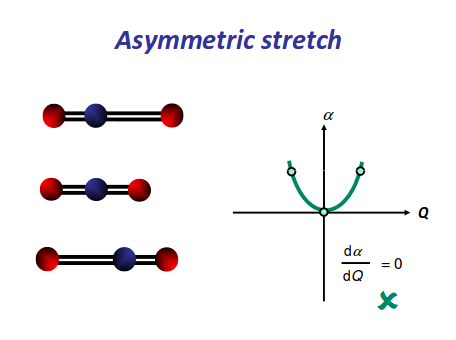
There is an induced dipole and thus a change in dipole moment (giving an uneven electron distribution), so this is IR active. However, if one oxygen moves towards the carbon, and then the other moves away, either extreme is similarly polarizable, so it becomes a symmetric change in polarizability, which means it is Raman inactive.
Finally, the bending modes:
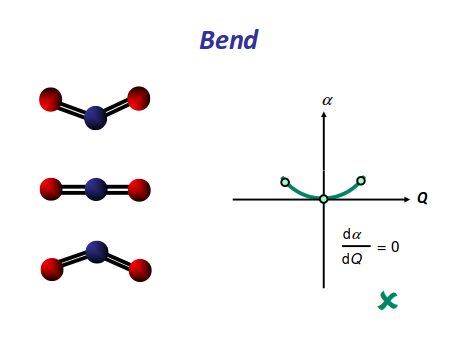
This bending has each oxygen either to one side of the carbon or to the other side. At this point we should recognize the induced dipole simply because the molecule bends, so this is IR active. However, since either extreme of the motion is similarly polarizable (they are similarly shaped snapshots), we again get a symmetric change in polarizability, which means this is Raman inactive.
IR AND RAMAN SPECTRA TEND TO BE COMPLEMENTARY
So when we look at the IR and Raman spectra layered together, we get:
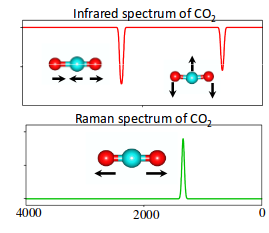
As predicted, the symmetric stretch showed up in the Raman spectrum, while the asymmetric stretch and the two bending vibrations showed up in the IR spectrum.
SIDENOTE: It's not crucial, but do note that a molecule COULD have peaks in both IR and Raman spectra, though usually if the Raman peak is weak, the IR peak is strong, and vice versa. As such, they make good complementary spectroscopic techniques.
As a general rule, when a molecule has centers of inversion, any Raman peaks it has are exclusive to Raman, and any IR peaks it has are exclusive to IR.
IR has a light source. So, what is the light source for Raman?
LIGHT SCATTERING CAUSES CHANGES IN VIBRATIONAL STATES
We're using a laser (such as a Nd:YAG 532 nm green laser) and firing it at the sample. The laser gives off a peak called the Rayleigh line.
The molecules might be in their ground vibrational state
While the molecules are in their unstable virtual states, they want to emit some photons to get back to a lower-energy, more stable state.
The photons that leave (or scatter) cause a Stokes shift and an Anti-Stokes shift, which are measured at an angle from the plane-polarized laser radiation.
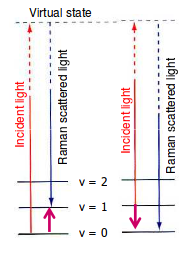
In the above diagram:
- The left event, the Stokes shift, is when the scattered photon is lower in energy than the incoming photon, thus leaving the molecule in a higher-energy state than when it started.
- The right event, the Anti-Stokes shift, is when the scattered photon is higher in energy than the incoming photon, thus leaving the molecule in a lower-energy state than when it started.
You can see that for the Stokes shift, the molecule started at
RELATING THE RAMAN SPECTRUM BACK TO THE IR SPECTRUM
On the Raman spectrum, you have the laser line at, say,
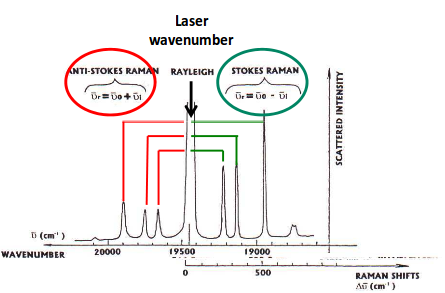
Since we fired a powerful laser, it must be accounted for when determining the frequencies of each peak.
If you take the laser frequency in

