What is the acceleration of the system and the tension in the ropes joining the masses in the following diagram?
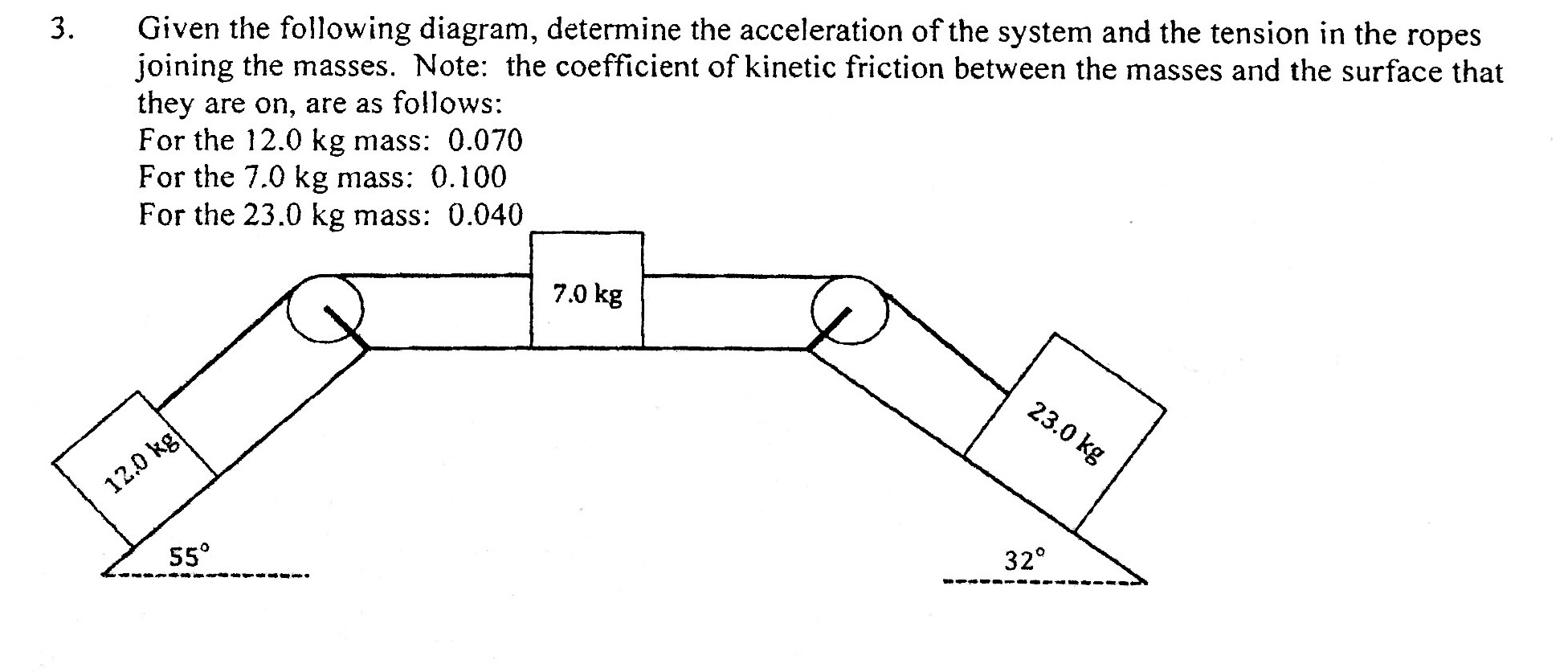
1 Answer
To 3sf we have
# a = 0.191 ms^-2#
# T_1 = 103 N#
# T_2 = 111 N #
Explanation:
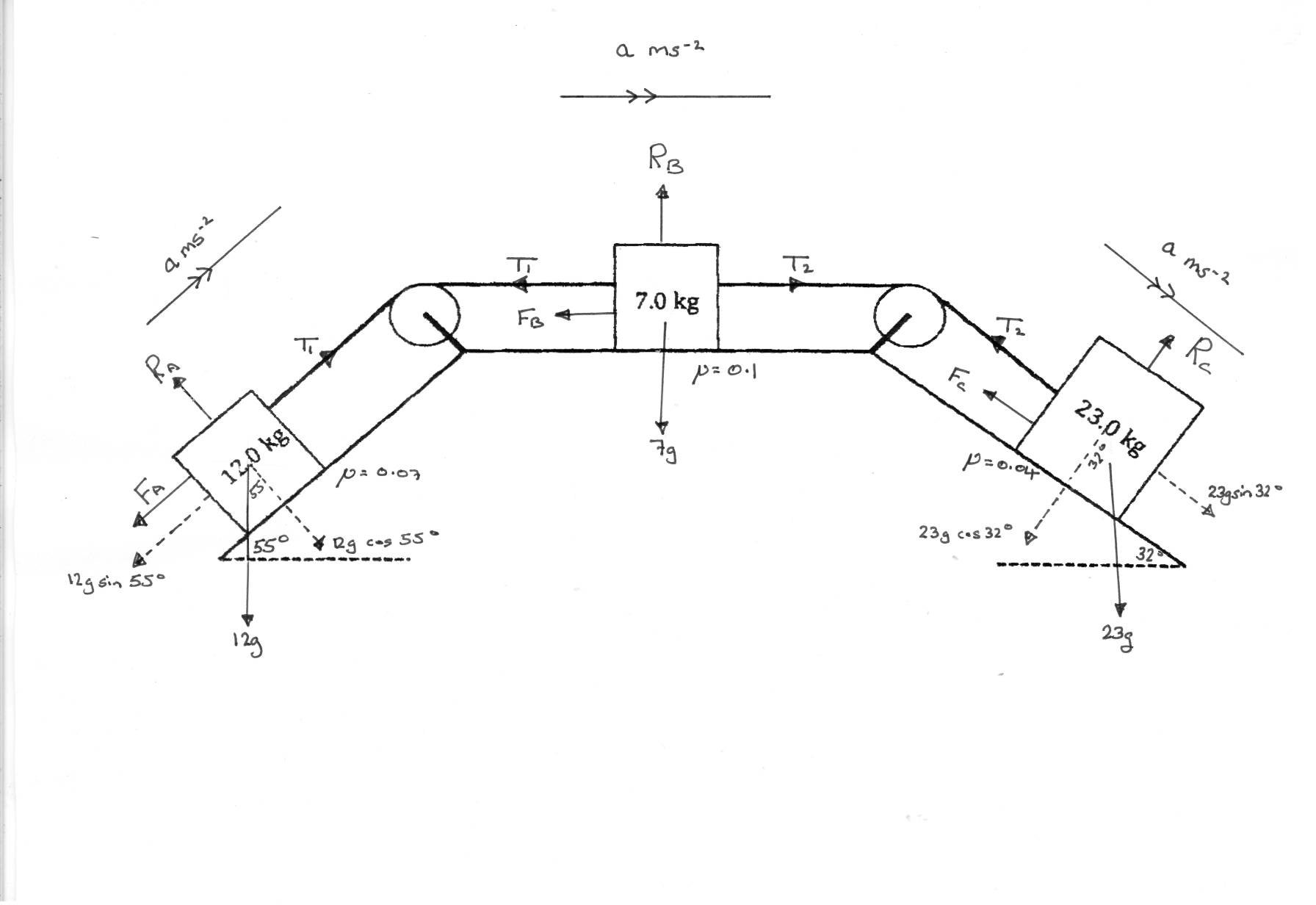
Assumptions
In order to answer this question we have to make a few assumptions.
1) The ropes are non-elastics (As we assume the tension in the rope is the same either side of the pulleys)
2) The pulleys are smooth (so that is no friction between the rope and the pulleys)
3)
Laying Out The Problem
The forces have been drawn on the diagram, I will use the symbols
It should be clear this system will not stay in equilibrium, rather objects
Reaction Forces
The first thing we can do is calculate the reaction forces for each of the objects. We need to do this s the friction force is related to the reaction, by
If we apply NSL to A perpendicular to the slope we get;
# 12gcos55 - R_A=0 => R_A = 12gcos55 #
Similarly for B and C we get:
# R_B = 7g#
# R_C = 23gcos32#
Consider Object A
If we apply NSL upwards parallel to the slope we get;
# T_1 - F_A - 12gsin55 = 12a #
# :. T_1 - mu_AR_A - 12gsin55 = 12a #
# :. T_1 - (0.07)(12gcos55) - 12gsin55 = 12a #
# :. T_1 - 0.84gcos55 - 12gsin55 = 12a #
# :. T_1 = 12a + 0.84gcos55 + 12gsin55 # ..... [1]
Consider Object C
If we apply NSL downwards parallel to the slope we get;
# 23gsin32 - T_2 - F_C = 23a #
# :. 23gsin32 - T_2 - mu_CR_C = 23a #
# :. 23gsin32 - T_2 -(0.04)(23gcos32) = 23a #
# :. 23gsin32 - T_2 -0.92gcos32 = 23a #
# :. T_2 = 23gsin32 -0.92gcos32 - 23a # ..... [2]
Consider Object B
If we apply NSL parallel to the slope we get;
# T_2 - T_1 - F_B = 7a #
# T_2 - T_1 - mu_BR_B = 7a #
# T_2 - T_1 - (0.1)(7g) = 7a #
# T_2 - T_1 - 0.7g = 7a # ..... [3]
Now if we substitute [1] and [2] into [3] we get:
# 23gsin32 -0.92gcos32 - 23a - (12a + 0.84gcos55 + 12gsin55) - 0.7g = 7a #
# :. 23gsin32 -0.92gcos32 - 23a - 12a - 0.84gcos55 - 12gsin55 - 0.7g = 7a #
# :. 42a = 23gsin32 -0.92gcos32 - 0.84gcos55 - 12gsin55 - 0.7g #
# :. a = g/42{23sin32 -0.92cos32 - 0.84cos55 - 12sin55 - 0.7) #
# :. a = 0.191339 ... ms^-2#
From [1] we have
# T_1 = 12(0.191339 ...) + 0.84gcos55 + 12gsin55 #
# :. T_1 = 103.350036 ... #
From [2] we have;
# T_2 = 23gsin32 -0.92gcos32 - 23(0.191339 ...) #
# :. T_2 = 23gsin32 -0.92gcos32 - 23(0.191339 ...) #
# :. T_2 = 111.453731 ... #
Hence, to 3sf we have
# :. a = 0.191 ms^-2#
# :. T_1 = 103 N#
# :. T_2 = 111 N #

