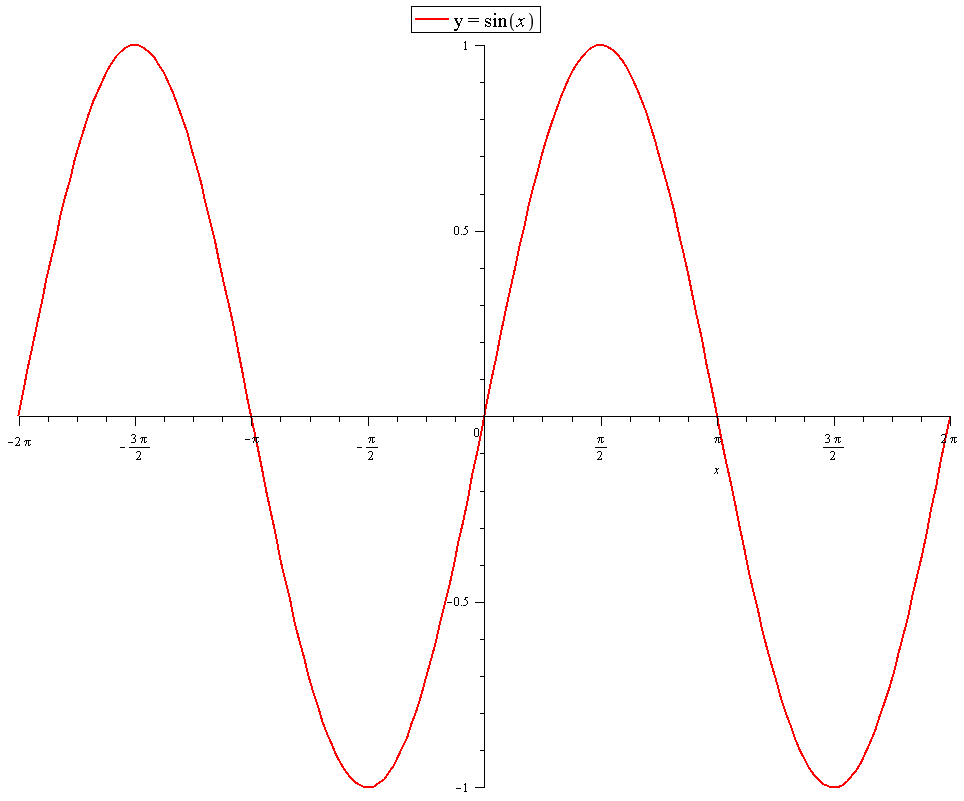
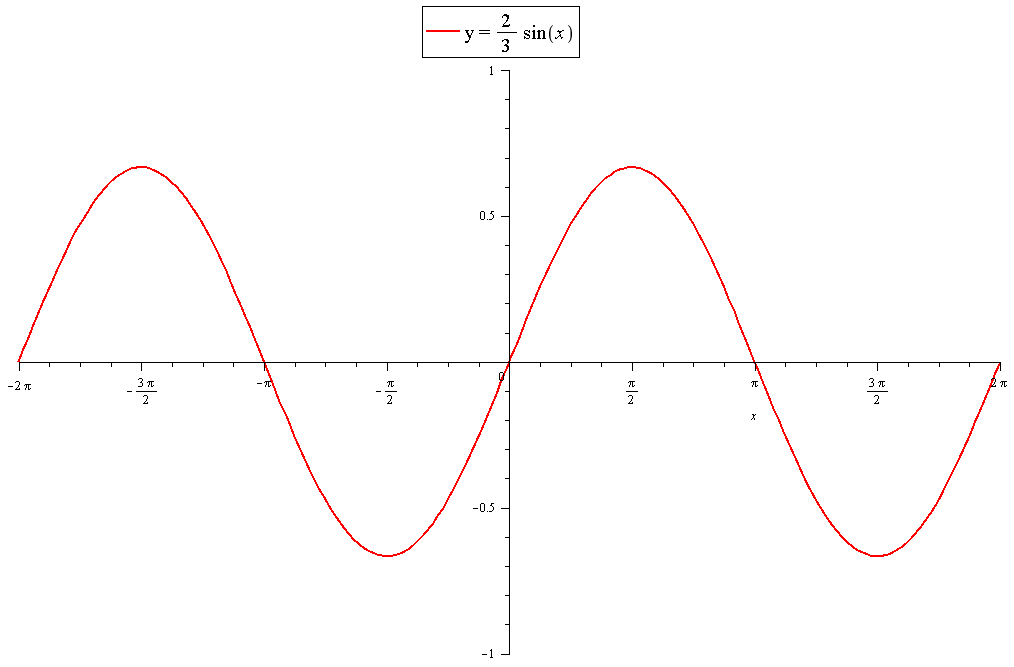
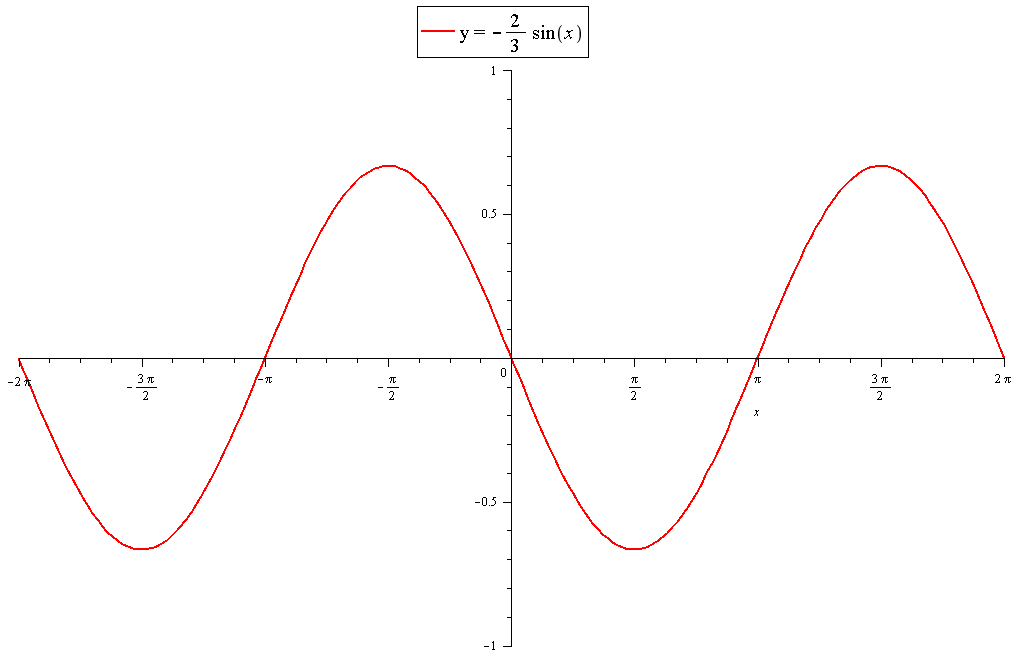
What is the amplitude of #y=-2/3sinx# and how does the graph relate to #y=sinx#?
1 Answer
Feb 11, 2018
See below.
Explanation:
We can express this in the form:
Where:
#color(white)(88)bba# is the amplitude.#color(white)(88)bb((2pi)/b)# is the period.#color(white)(8)bb(-c/b)# is the phase shift.#color(white)(888)bb(d)# is the vertical shift.
From our example:
We can see the amplitude is
So:
Graphs of the different stages: