Question

What is the amplitude of `y=cos(-3x)` and how does the graph relate to `y=cosx`?

Answer 1

Exploring Graphs available:

Amplitude

`color(blue)(y = Cos(-3x) = 1)`

`color(blue)(y = Cos(x) = 1)`

Period

`color(blue)(y = Cos(-3x) = (2Pi)/3)`

`color(blue)(y = Cos(x) = 2Pi`

Explanation:

The Amplitude is the height from the center line to the peak or to the trough.

Or, we can measure the height from the highest to lowest points and divide that value by `2.`

A Periodic Function is a function that repeats its values in regular intervals or Periods.

We can observe this behavior in the graphs available with this solution.

Note that the trigonometric function Cos is a Periodic Function.

We are given the trigonometric functions

`color(red)(y = cos(-3x))`

`color(red)(y = cos(x))`

The General Form of the equation of the Cos function:

`color(green)(y = A*Cos(Bx - C) + D)`, where

A represents the Vertical Stretch Factor and its absolute value is the Amplitude.

B is used to find the Period (P):`" "P = (2Pi)/B`

C, if given, indicates that we have a place shift BUT it is NOT equal to `C`

The Place Shift is actually equal to `x` under certain special circumstances or conditions.

D represents Vertical Shift.

The trigonometric function available with us is

`color(red)(y = cos(-3x))`

Observe the graph given below:

`color(red)(y = cos(x))`

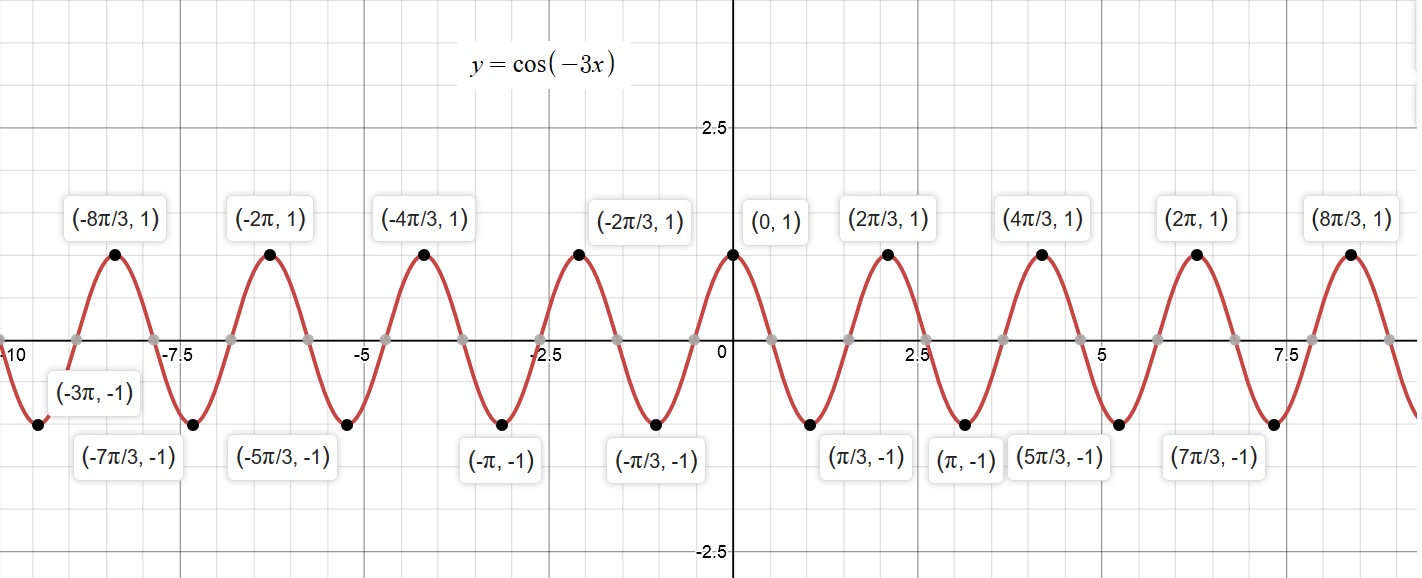
Observe the graph given below:

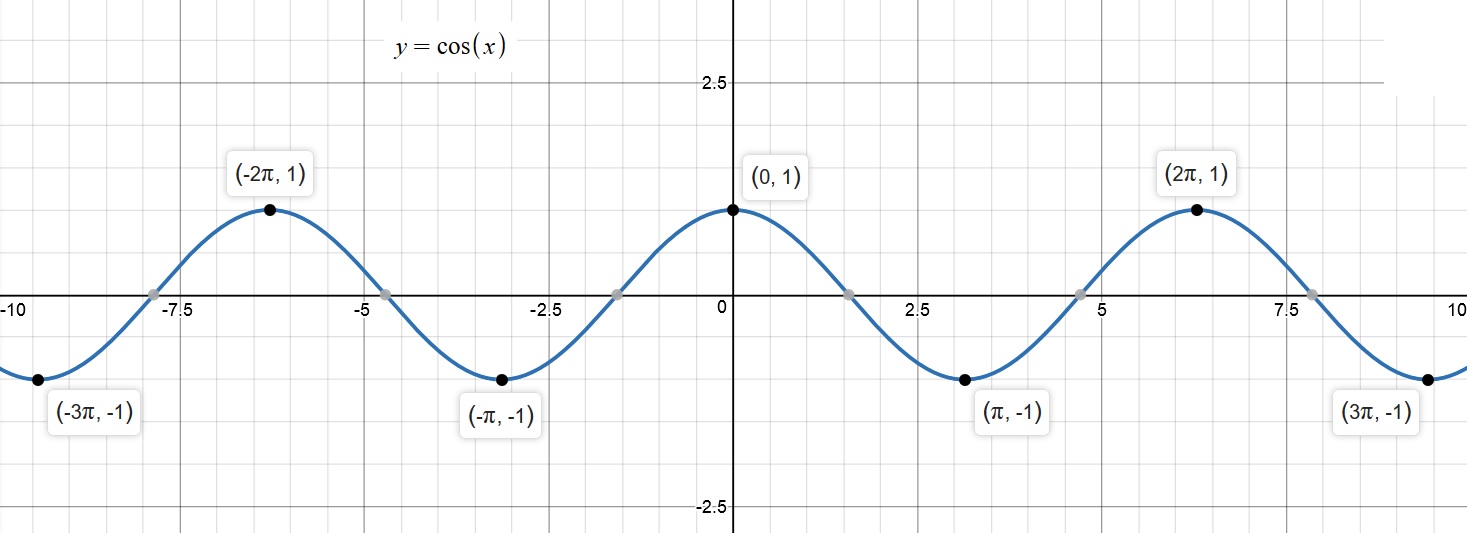
Combined Graphs of the trigonometric functions

`color(red)(y = cos(-3x))`

`color(red)(y = cos(x))`

are available below for establishing relationship:

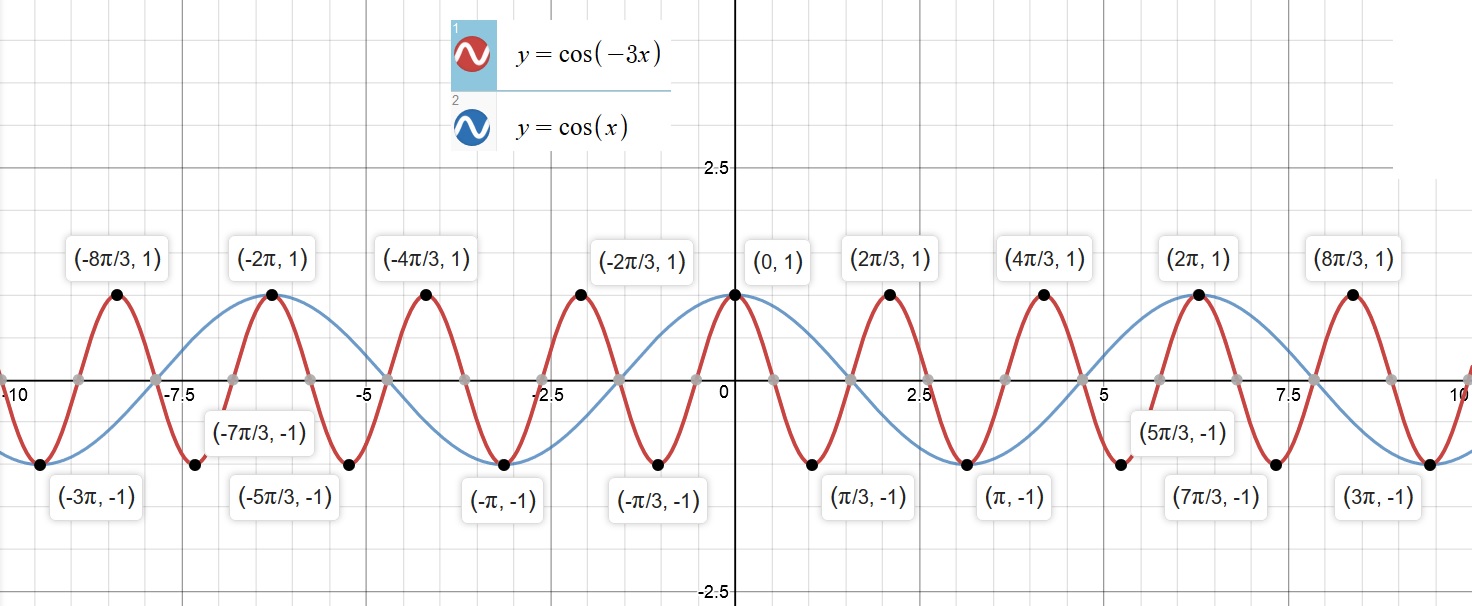
How does the graph of `color(red)(y=Cos(-3x)` relate to the graph of `color(red)(y = Cos(x)?`

Exploring the graphs above, we note that:

Amplitude

`color(blue)(y = Cos(-3x) = 1)`

`color(blue)(y = Cos(x) = 1)`

Period

`color(blue)(y = Cos(-3x) = (2Pi)/3)`

`color(blue)(y = Cos(x) = 2Pi`

We also note the following:

the graph of `color(blue)(y = cos(x))` is symmetric about the y-axis, because it is an Even function.

the domain of each function is `(-oo, oo)` and range is `(-1, 1)`