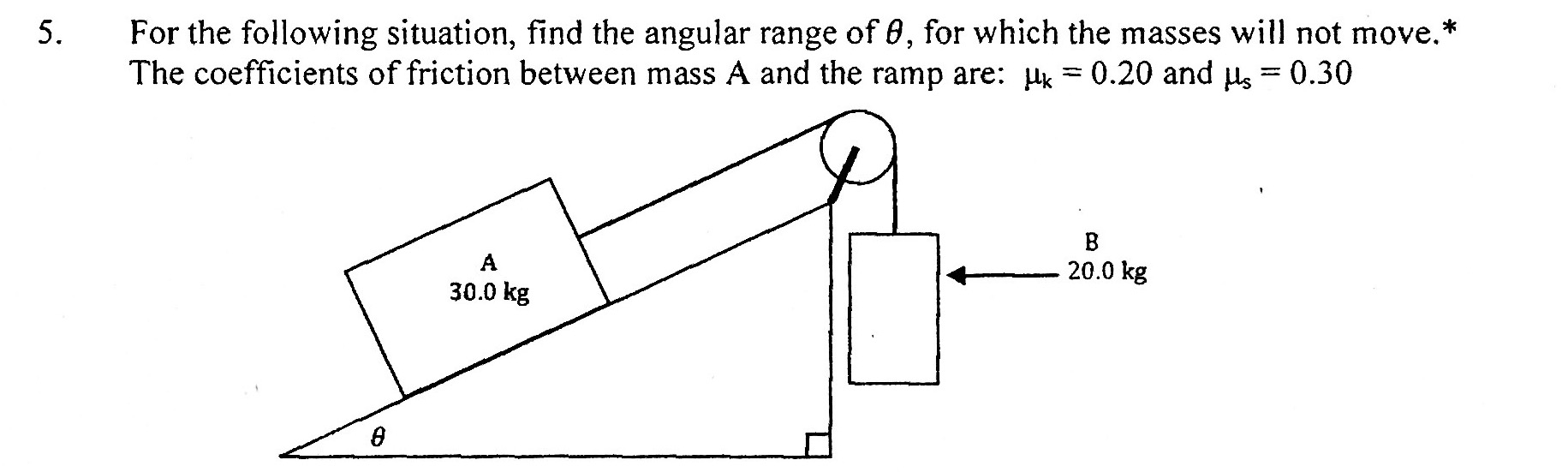
What is the angular range for #theta#, for which the masses will not move in the following diagram?
1 Answer
First considering the situation when the block A tends to move downward along the inclined plane.In this situation the force of friction as well as weight of block B together will balance the downward force on block A.
Taking acceleration due to gravity
So
Let 10/sqrt109=cosalpha and 3/sqrt109=sinalpha#
This means
The above equation becomes
Again considering the situation when the block A tends to move upward along the inclined plane.In this situation the force of friction as well as downward force on block A together will balance the downward force on block B.
So
Similar manner we get
Here
So when

