What is the area of an isosceles triangle with a base of 6 and sides of 4?
2 Answers
Sep 8, 2015
The area of a triangle is
The height is
So we have that
Sep 8, 2015
I found
Explanation:
Consider your triangle:
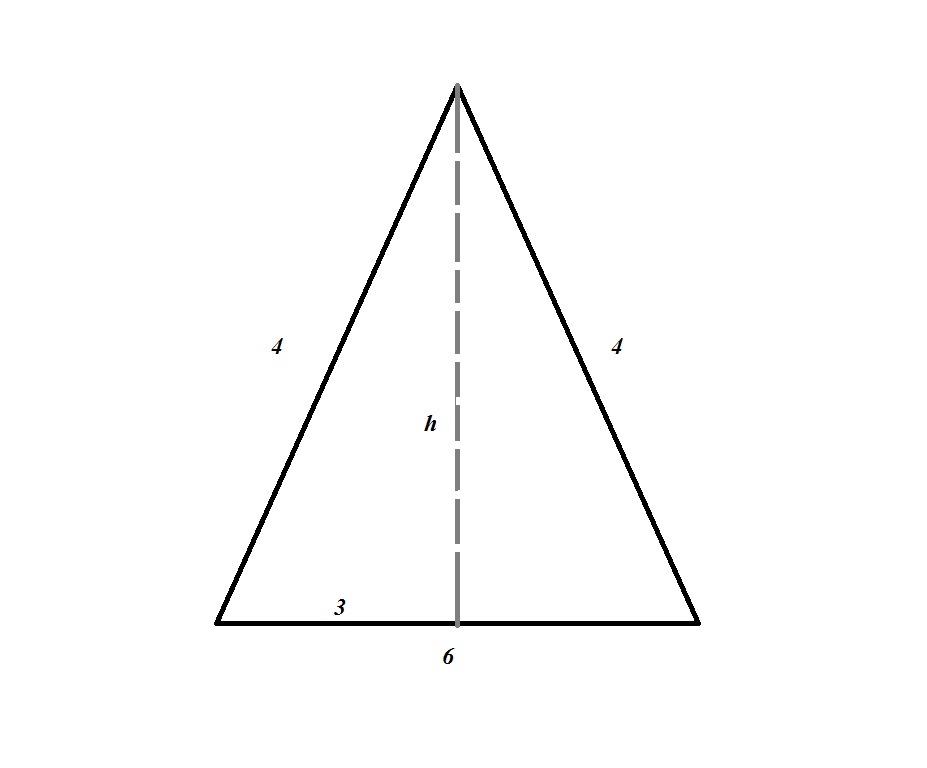
You can use Phytagoras Theorem to find
So the area will be:


