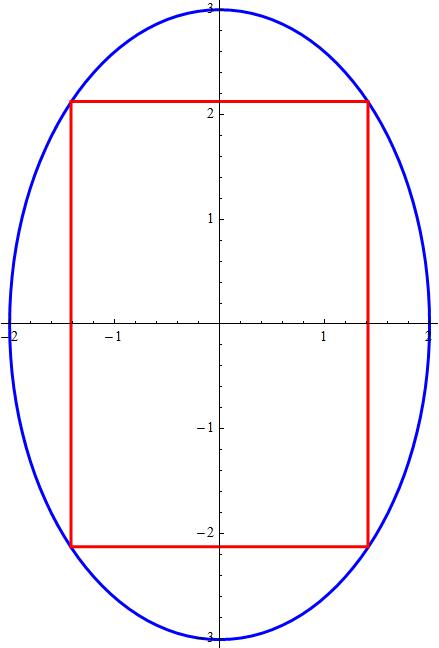
What is the area of the largest rectangle that can be inscribed in the ellipse: #9(x^2) + 4(y^2) = 36#?
1 Answer
Jun 16, 2016
Explanation:
The problem can be posed as:
Find Max
Making now
Find
The lagrangian for determination of stationary points is
The stationarity conditions are
or
Solving for
so