Question

What is the area of the largest rectangle that can be inscribed under the graph of y=2 cos x for -π /2 ≤x ≤π /2?

Answer 1

Maximum area is `2.244 " unit"^2` (3dp)

Explanation:

I assume that you man bounded by the x-axis also, otherwise the largest rectangle would be unbounded and therefore infinite.

This is a diagram depicting the problem:

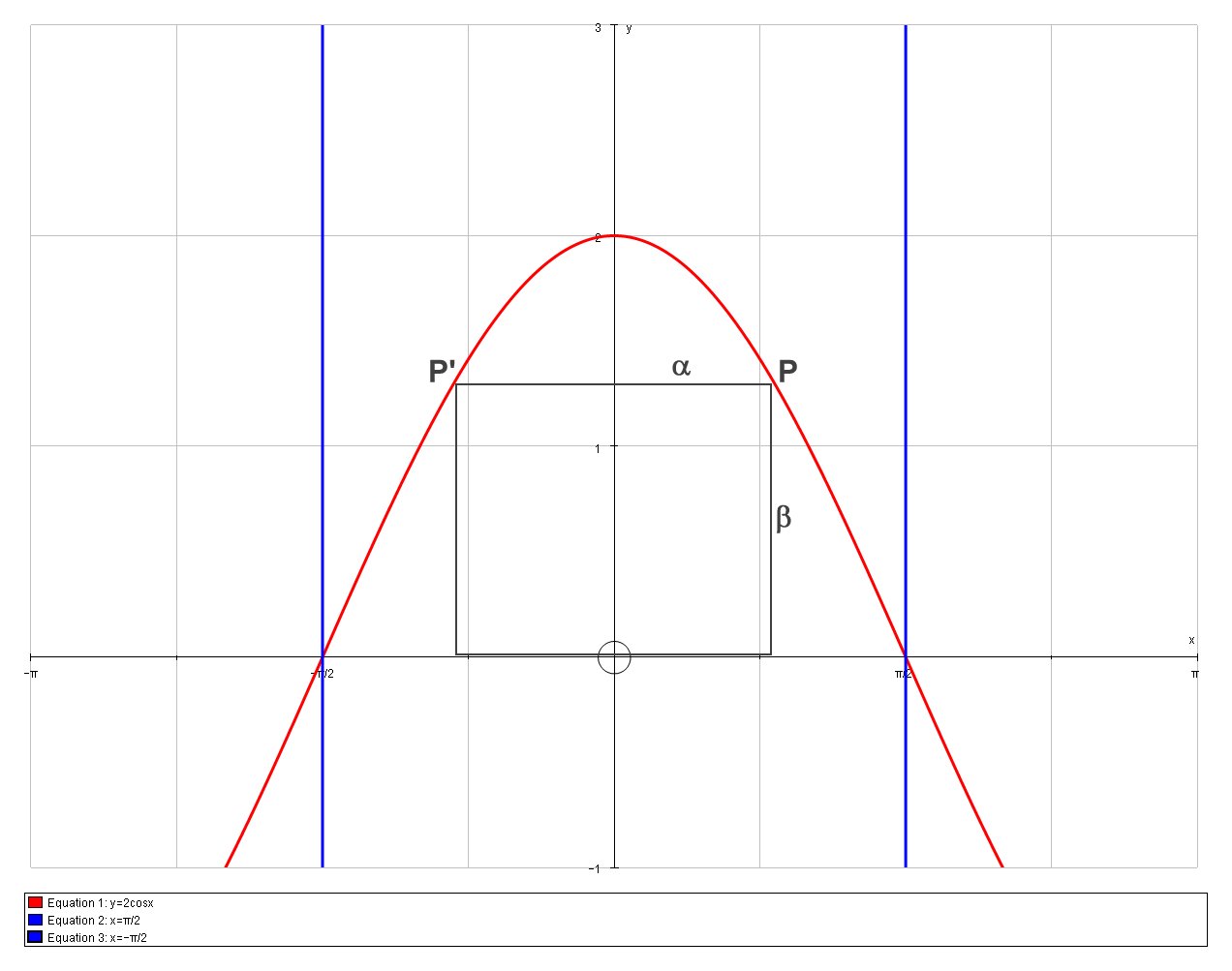
Where `P(alpha,beta)` is the point in Quadrant 1 where the rectangle intersects the curve `y=2cosx`, and `P'(-alpha,beta)` is the corresponding point in quadrant 2.

Let us set up the following variables:

`{ (alpha, x"-coordinate of point "P), (beta, y"-coordinate of point "P),(A, "Total Area of inscribed rectangle") :}`

Our aim is to find `A`, as a function of a single variable and to maximize the total area, `A` (It won't matter which variable we do this with as we will get the same result). ie we want a critical point of `A` wrt the variable.

As `P` lies on the curve `y=2cosx`, we have:

`beta = 2cos alpha \ \ \ \ \ ..... [1]`

And the total Area is that of a rectangle of width `2alpha` and height `beta`, so:

`A = 2 alpha beta`
`\ \ \ = 2 alpha (2cos alpha) \ \ \ \ \` (from [1] )
`\ \ \ = 4 alpha cos alpha`

We now have the Area, `A`, as a function of a single variable `alpha`, so differentiating wrt `alpha` (using the product rule) we get:

`(dA)/(d alpha) = (4alpha)(-sin alpha) + (4)(cos alpha)`
`\ \ \ \ \ \ = 4(cos alpha - alpha sin alpha )`

At a critical point we have `(dA)/(d alpha) =0 =>`

`4(cos alpha - alpha sin alpha ) = 0`
`:. cos alpha - alpha sin alpha = 0`

In order to solve this equation we use Newton-Rhapson which gives `alpha =0.860333589 ...`

With this value of `alpha` we have:

`beta = 1.30436924 ...`
`A = 2.24438535 ...`

We can visually verify that this corresponds to a maximum by looking at the graph of `y=A(alpha)`:

graph{4xcosx [-4, 4, -5.5, 5.5]}

So maximum area is `2.244 " unit"^2` (3dp)