What is the area of the region in the first quadrant enclosed by the graphs of y = cosx, y= x, and the y -axis?
1 Answer
Explanation:
To find the area between two curves, find the integral of the difference between the two functions over the desired interval.
That is a mouthful, so it is probably best to explain using a graph:
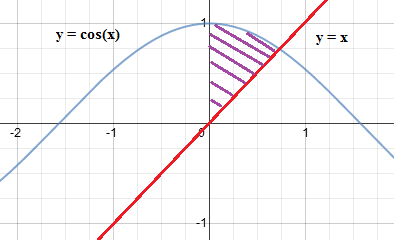
We are looking for the purple area between these two curves. First, let's figure out where
Unfortunately, there is not an easy way to find the intersection of these two functions by hand. Using a graphing calculator, it can be seen that
Now, let's integrate:
Function 1:
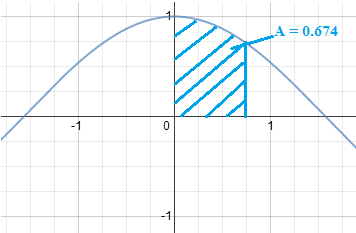
Function 2:
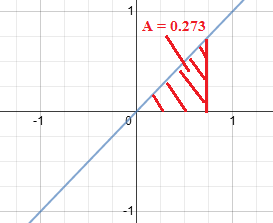
Combining the two, we get that the area between
Graphically, we can see this as what is shown at the beginning.

