What is the area of this regular hexagon?
2 Answers
Area =
Explanation:
We will Use the area of the hexagon formula
Now what is is an apothem;
The apothem (sometimes abbreviated as apo) of a regular polygon is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides.
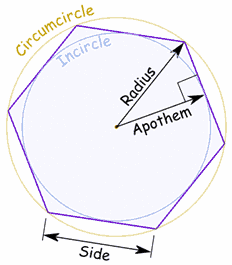
Apothem
Now for a regular polygon of n sides the perimeter is
Finally lets plug in ;
Area =
Additionally there are multiple ways to find area of a hexagon
1)Use formula ; If you know a side of a regular hexagon you can use this;

2) Using the apothem method;

For more on this visit;
http://www.dummies.com/how-to/content/how-to-calculate-the-area-of-a-regular-hexagon.html
The area is approximately
Explanation:
As this hexagon is regular, you can divide it into
Please note that all those triangles are isosceles. All angles of the hexagon are
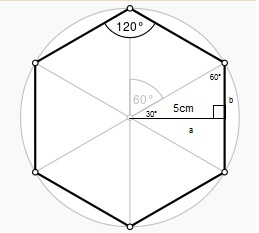
As you see in the picture, each of those 6 "big" triangles can be divided into two small triangles with the angles
To compute the area of the small right angle triangle, you need just the length of
This you can do with
This means that the area of the small right angle triangle is
There are
Hope that this helped!


