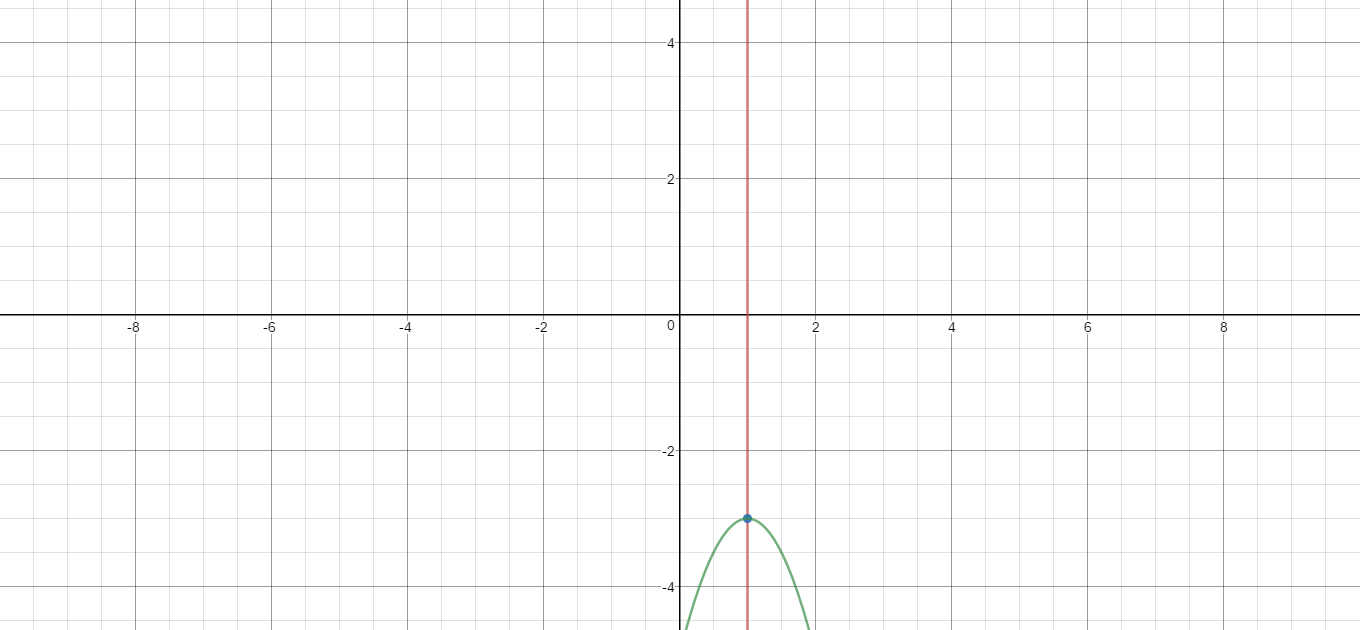
What is the axis of symmetry and vertex for the graph #y=-2x^2+4x-5#?

Question

5748 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-17T18:41:02

The equation of the axis of symmetry is #x=1# and the vertex is #(1,-3)#. Please see the explanation.

When given an equation of the form, #y = ax^2 + bx +c#, the equation of the axis of symmetry line is:

#x = -b/(2a)#

This is, also, h; the x coordinate of the vertex:

#h = -b/(2a)#

The y coordinate of the vertex, k, is the value of the function evaluated at h:

#k = y(h)#

For the given equation, #a = -2, b = 4 and c = -5#

The equation of the axis of symmetry is:

#x = -4/(2(-2)#

#x = 1#

This is, also, the x coordinated of vertex:

#h = 1#

The y coordinate of the vertex is:

#k = -2(1)^2 + 4(1)-5#

#k = -3#

The vertex is #(1,-3)#

Here is a graph of, the function, the axis of symmetry, and the vertex.

Desmos.com