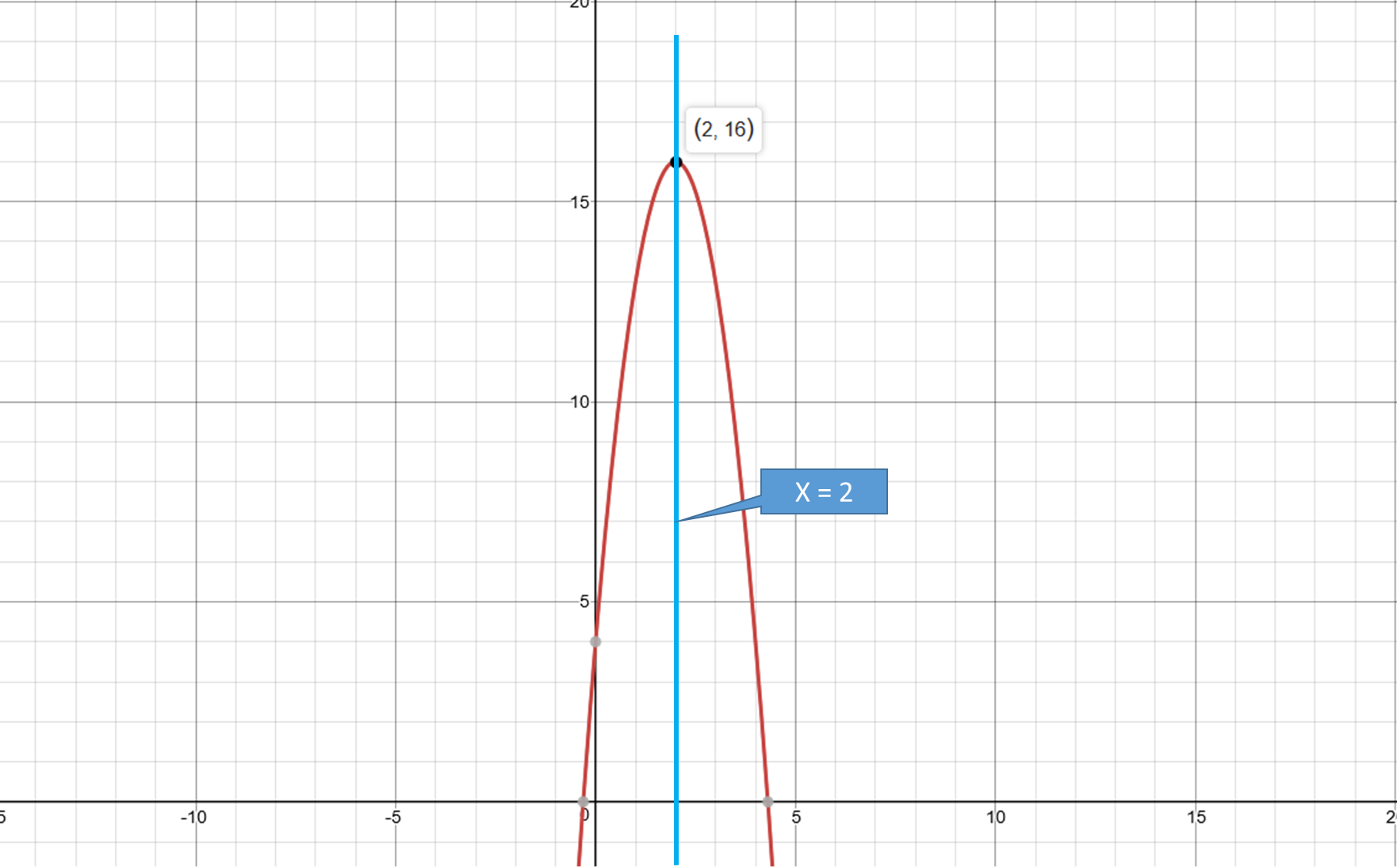
What is the axis of symmetry and vertex for the graph #y = -3x^2 + 12x + 4#?
2 Answers
Jun 3, 2018
aos = 2
vertex = (2,16)
Explanation:
In the form
Axis of symmetry (aos) is:
Remember
Vertex is:
vertex
graph{-3x^2 + 12x + 4 [-16.71, 23.29, -1.6, 18.4]}
Jun 3, 2018
Vertex -
#(2,16)#
Axis of symmetry
#x=2#
Explanation:
Given -
#y=-3x^2+12x+4#
Vertex -
#x=(-b)/(2a)=(-12)/(2xx-3)=(-12)/(-6)=2#
At
#y=-12+24+4=16#
#(2,16)#
Axis of symmetry
#x=2#