Consider the standard form of #y=ax^2+bx+c#
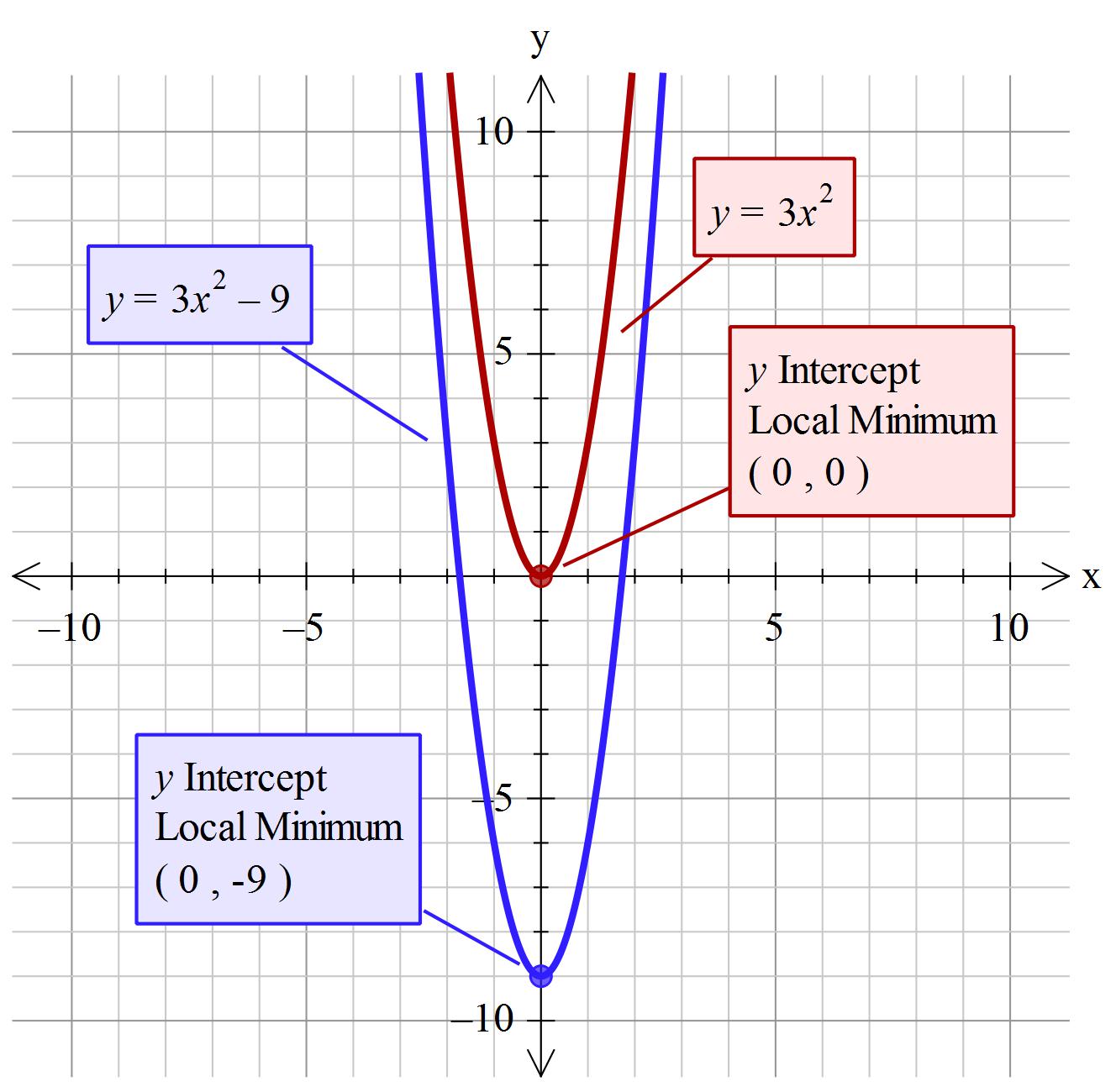
Given:#" "y=3x^2-9#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("General shape of the graph")#
The three in front of #x^2# is positive so the graph is of general shape #uu#. Suppose it was -3. Then the general shape for that scenario would be #nn#
So the shape of #uu# means we have a minimum.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Axis of symmetry")#
There is no term for the equation part #bx# thus the graphs axis of symmetry is #x=0#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Vertex")#
Suppose you just had #color(brown)(y=3x^2)# then the minimum would be at #color(brown)(y=0)#
However, we have #color(brown)(y=3x^2)color(blue)( -9)# so the vertex lowers by 9.
#color(green)(y_("vertex")->color(brown)(y=0color(blue)(-9))=-9)#