What is the axis of symmetry and vertex for the graph #y = x ^2 - 4 x + 3#?

Question

1368 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-05-26T06:11:22

Vertex #(2, -1)#
Axis of symmetry #x=2#

Given -

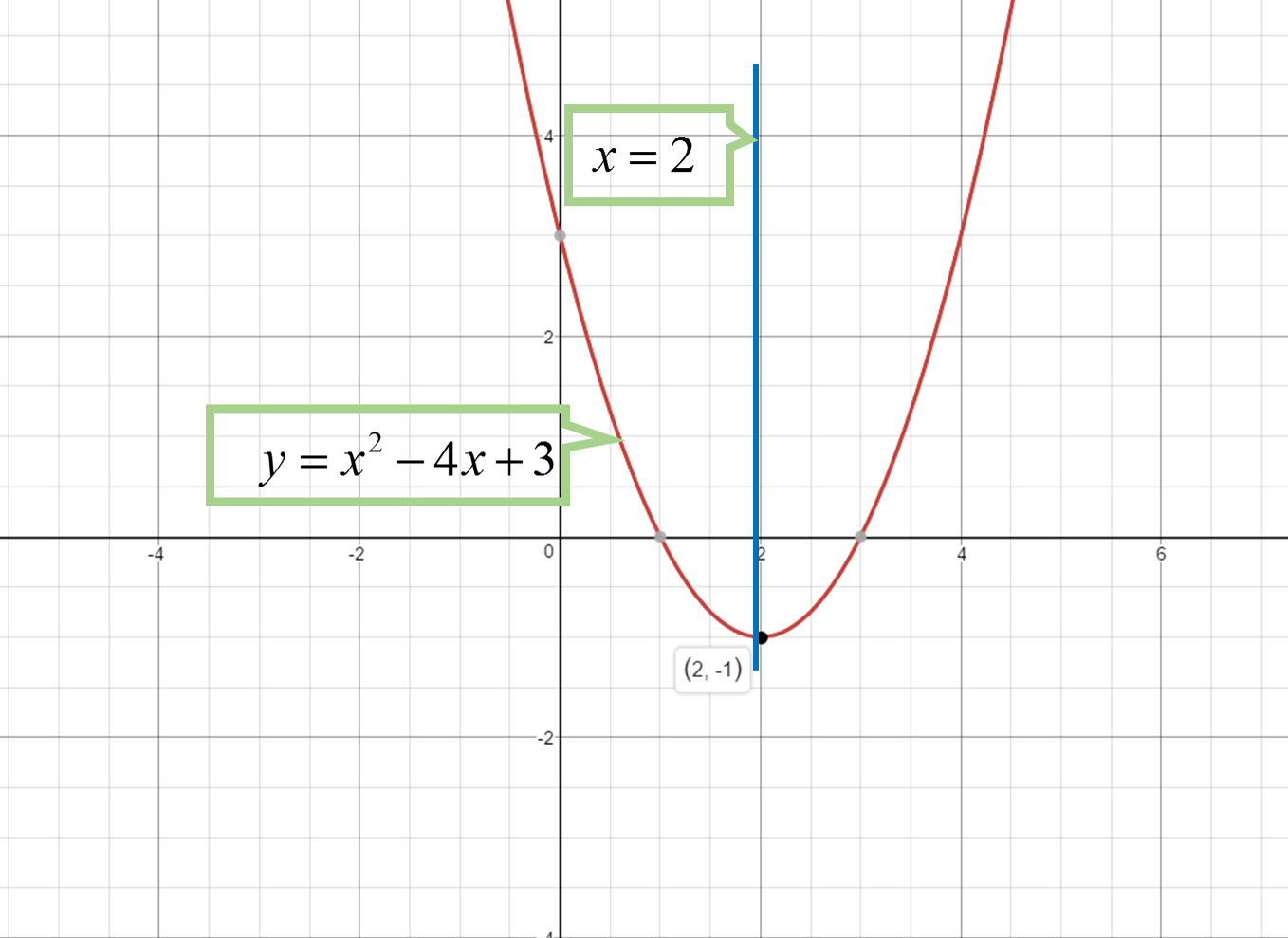
#y=x^2-4x+3#

Vertex -
x-coordinate of the vertex

#x=(-b).(2a)=(-(-4))/(2xx1)=4/2=2#

y-coordinate of the vertex

#y=2^2-4(2)+3=4-8+3=-1#

Vertex #(2, -1)#

Axis of symmetry #x=2#

enter image source here

Answer 2 · 2017-05-26T08:16:43

#X=2#

#(2,-1)#

Another way of finding the axis and vertex is to complete the square

#y=x^2-4x+3#

#y=(x-2)^2-1#

for the vertex find the #x" "# value that makes the bracket #=0#

#x=2=>y=-1#

vertex #(2,-1)#

axis of symmetry simply the the x-value above #X=2#

with the graph as before