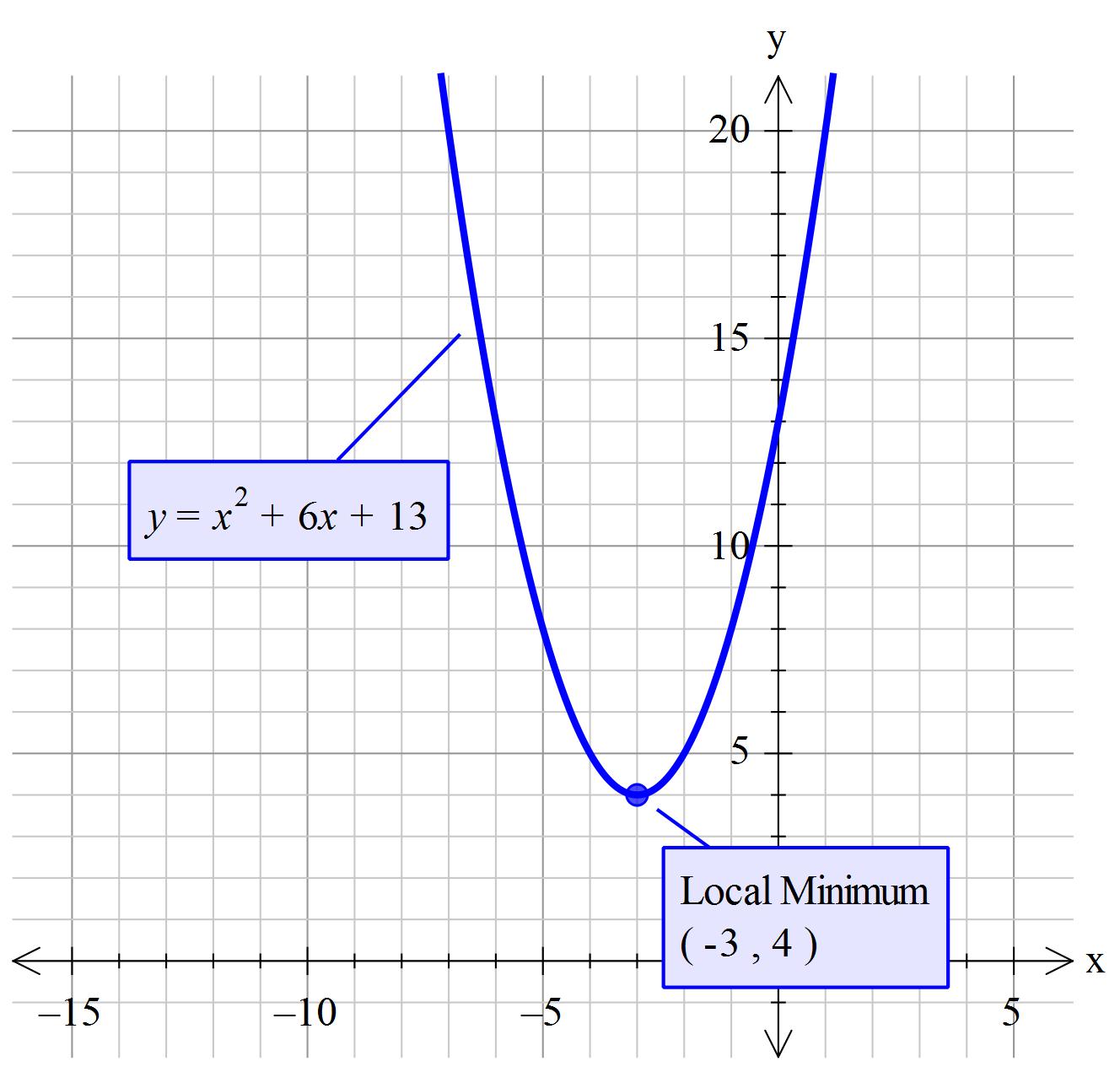
What is the axis of symmetry and vertex for the graph #y = x^2 + 6x + 13#?

Question

4727 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-05-03T12:53:10

Axis of symmetry -> x = -3

Vertex -> (x,y)-> (-3, 4 )

Consider the general form #y=ax^2+bx+c#

Write the general form as #y=a(x^2+b/ax)+c#

In your case #a=1#

#color(blue)(x_("vertex")=(-1/2)xxb/a -> (-1/2)xx6 = -3)#

#color(blue)("axis of symmetry "->x=-3)#

To find #y_("vertex")# substitute #x=-3# in the original equation.

#=> y_("vertex")=(-3)^2+6(-3)+13#

#color(blue)(=> y_("vertex")=+4)#

#color(brown)("Vertex" ->(x,y)->(-3,4))#
Tony B