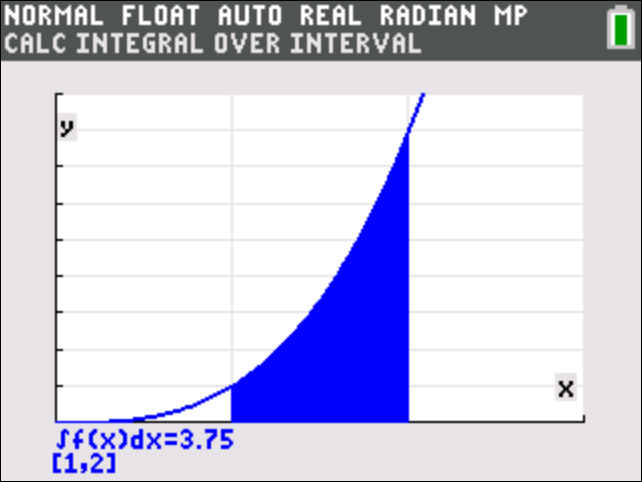
What is the definite integral of #x^3# from 1 to 2?
1 Answer
Sep 10, 2014
Increment the exponent from 3 to 4. Also use the 4 as the denominator. Then substitute the boundaries into the function, where you have to subtract the lower boundary once substituted from the upper boundary once substituted. Then use basic algebra to evaluate.
This image a graph of the function