The distance between two points
#(x_1, y_1, z_1)#
and
#(x_2, y_2, z_2)#
in #RR^3# (three dimensions) is given by
#"distance" = sqrt((x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2)#
Applying it to the problem at hand, we get the distance between #(0, 0, 8)# and #(9, 2, 0)# as
#"distance" = sqrt((9-0)^2 + (2-0)^2 + (0-8)^2) = sqrt(81 + 4 + 64) = sqrt(149)#
.
.
.
The following is an explanation as to where the distance formula comes from, and is not necessary for understanding the above solution.
The distance formula given above looks suspiciously similar to the distance formula in #RR^2# (two dimensions):
#"distance" = sqrt((x_2-x_1)^2 + (y_2-y_1)^2)#
which comes from a simple application of the Pythagorean theorem, by drawing a right triangle between two points with the legs parallel to the #x# and #y# axes.
It turns out, the #RR^3# version can be derived in a similar manner. If we use (at most) 3 lines to connect two points, going parallel to the #x#, #y#, and #z# axes, we get a box with the points as opposite corners. So, let's figure out how to calculate the distance across the diagonal of a box.
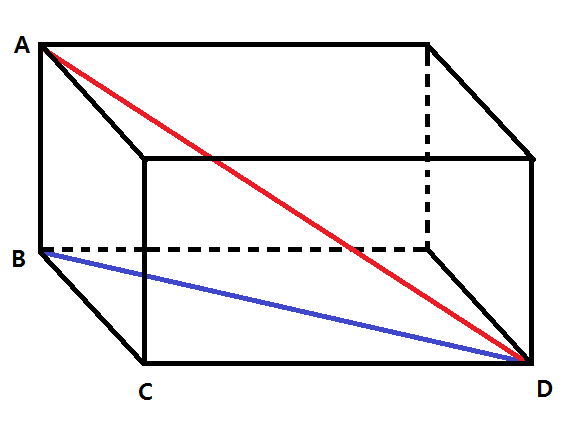
We are trying to figure out the length of the red line #color(red)(AD)#
As this is the hypotenuse of the triangle #ABD#, from the Pythagorean theorem:
#(color(red)(AD))^2 = (AB)^2 + (color(blue)(BC))^2#
#=> color(red)(AD) = sqrt((AB)^2 + (color(blue)(BC))^2)" (i)"#
Unfortunately, we don't have the length of #color(blue)(BD)# as a given. To get it, we must again apply the Pythagorean theorem, this time to the triangle #BCD#.
#(color(blue)(BD))^2 = (BC)^2 + (CD)^2" (ii)"#
As we only need the square of #color(blue)(BD)#, we can now substitute #("ii")# into #("i")#:
#color(red)(AD) = sqrt((AB)^2 + (BC)^2 + (CD)^2)#
Finally, if we have #A# at #(x_1, y_1, z_1)# and #D# at #(x_2, y_2, z_2)#, then we have the lengths
#CD = |x_2 - x_1|#
#BC = |y_2 - y_1|#
#AB = |z_2 - z_1|#
Substituting these into the the above gives us the desired result.
As an extra note, while we can only easily do geometric proofs in up to 3 dimensions, mathematicians have generalized distance in #RR^n# (#n# dimensions). The distance between
#(x_1, x_2, ..., x_n)# and #(y_1, y_2, ..., y_n)# is defined as
#sqrt(sum_(k=1)^n(y_k - x_k)^2)#
which matches the pattern from #RR^2# and #RR^3#.


