What is the distance between #(–3, –2)# and #(5, 2)#?

Question

4482 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-02T04:08:01

#4sqrt5#

The distance, #r#, between two points with coordinates #(x_1,y_1)# and #(x_2,y_2)# is given by

#r = sqrt((x_1 - x_2)^2 + (y_1 - y_2)^2)#

mathsfirst.massey.ac.nz

It is an application of Pythagoras Theorem.

Therefore, the distance between #(-3,-2)# and #(5,2)# is

#sqrt((-3 - 5)^2 + (-2 - 2)^2) = sqrt(64+16)#

#= sqrt80#

#= 4sqrt5#

Answer 2 · 2016-04-02T08:24:38

#4sqrt5#

#color(blue)((-3,-2)and(5,2)#

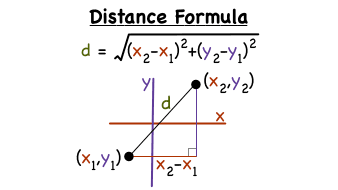
enter image source here

So,

#color(purple)(x_1=-3,x_2=5#

#color(purple)(y_1=-2,y_2=2#

#:.d=sqrt((-3-5)^2+(-2-2)^2)#

#rarrsqrt((-8)^2+(-4)^2)#

#rarrsqrt(64+16)#

#rarrsqrt80#

#rarrsqrt(16*5)#

#color(green)(rArr4sqrt5#