What is the distance between #(8, 2) # and # (4, -5) #?
3 Answers
Explanation:
Explanation:
(8, 2) and (4, -5) are two points in a cartesian plane.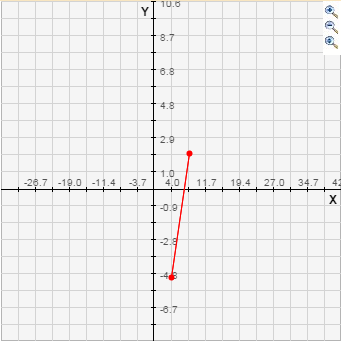
The line represents the distance between the points. The size of the line can be calculated using Pythagoras' formula:
Explanation:
The distance formula for Cartesian coordinates is
Where
Let
Hence the distance between the given points is



