What is the electron configuration of chromium?
2 Answers
The electron configuration for chromium is NOT
Interestingly enough, Tungsten is more stable with an electron arrangement of
Unfortunately, there is no easy way to explain these deviations in the ideal order for each element.
To explain Chromium's electron configuration, we could introduce:
- The exchange energy
#Pi_e# (a stabilizing quantum mechanical factor that is directly proportional to the number of pairs of electrons in the same subshell or very close-energy subshells with parallel spins) - The coulombic repulsion energy
#Pi_c# (a destabilizing factor that is inversely proportional to the number of electron pairs) - These combine to produce an overall pairing energy
#Pi = Pi_c + Pi_e# .
The former is stabilizing and the latter is destabilizing, as shown below (suppose configuration 2 is at pairing energy
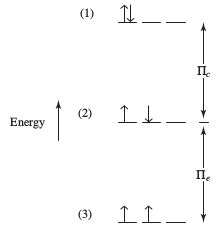
One explanation for Chromium, then, is that:
- The maximized exchange energy
#Pi_e# stabilizes this configuration (#3d^5 4s^1# ). The maximization comes from how there are#5# unpaired electrons, instead of just#4# (#3d^4 4s^2# ). - The minimized coulombic repulsion energy
#Pi_c# further stabilizes this configuration. The minimization comes from having all unpaired electrons in the#3d# and#4s# (#3d^5 4s^1# ), rather than one electron pair in the#4s# (#3d^4 4s^2# ). - The small-enough orbital size means that the electron density is not as spread out as it could be, which makes it favorable enough for a maximum total spin to give the most stable configuration.
However, Tungsten's
The more the electron distribution is spread out, the less electron-pair repulsion there is, and thus the lower
Thus, electron pairing is favorable enough for Tungsten.
There is no hard and fast rule for this, but that is an explanation that correlates with experimental data.
The electron configuration of chromium is
Explanation:
The typical energy level diagram you see in text books showing the 4s below the 3d is ok up to calcium.
After that the 3d sub - shell falls below the 4s in energy but the difference is very small. Repulsive forces then tend to "push" electrons up into the larger 4s orbital where repulsion is less.
This is why the 4s electrons are lost first when the elements of the 1st transition series ionise.
This also explains why the electron structure of
The 4s electrons are the outer valence electrons which also define the atomic radius.



