What is the equation of the line that passes through #(-1,1) # and is perpendicular to the line that passes through the following points: #(-2,4),(-12,21) #?
2 Answers
Explanation:
Consider the two points
The straight line between them has the gradient:
The gradient of the perpendicular line is
So we have
So by substitution we get:
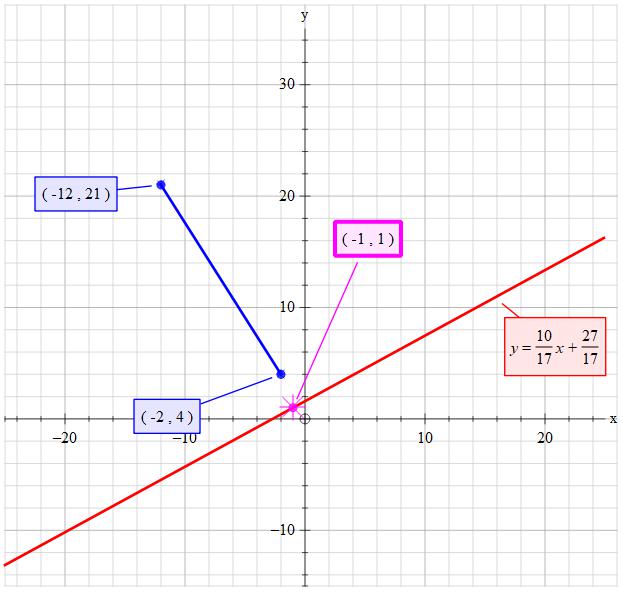
Equation of line is
Explanation:
The slope of the line passing through
is
The product of slopes of the pependicular lines is
line is
is
Equation of line is

