Question

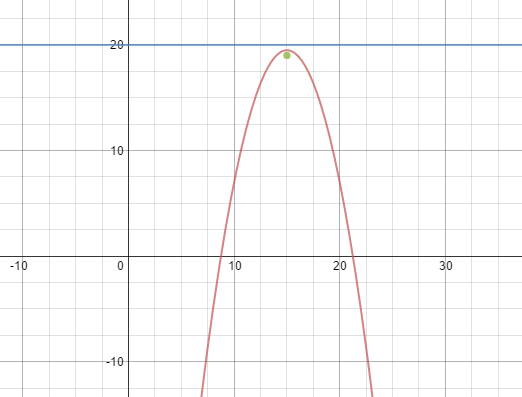
What is the equation of the parabola with a focus at (15,19) and a directrix of y= 20?

Answer 1

The directrix is above the focus, so this is a downward opening parabola.

Explanation:

The vertex will lie exactly halfway between the directrix and the focus:

`"vertex"=(15,19.5)`

The distance `p` between the vertex and the focus is `p=1/2`, so the absolute value of the coefficient `abs(a) = 1/(4p)= 1/2` Now, since we know the parabola opens downward, the sign on the coefficient must be negative.

Here is the final equation:

`y=-1/2(x-15)^2+19.5`

hope that helped