What is the equation of the porabola with a vertex at the origin and a directrix of x=4?
1 Answer
Oct 29, 2015
Explanation:
The focus is located on a line perpendicular to the directrix through the vertex and at an equal distance on the opposite side of the vertex from the directrix.
So, in this case the focus is at
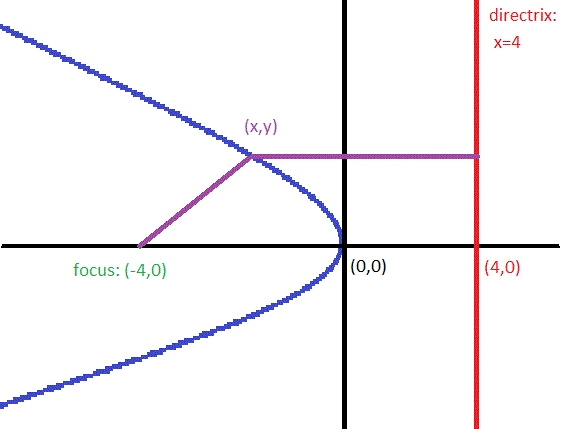
(Note: this diagram is not properly scaled)
For any point,
distance to focus = distance to directrix.
