Given #r(theta)# we have
#{
(x(theta)=r(theta)cos(theta)),
(y(theta)=r(theta)sin(theta))
:}#
#
{
(dx/(d theta) = -r(theta)sin(theta)+cos(theta)((dr)/(d theta))),
(dy/(d theta) = r(theta)cos(theta)+sin(theta)((dr)/(d theta)))
:}
#
but
#r(theta) = 2 cos(theta - 3 pi/4) + 2 sin(-theta + 3 pi/2)#
then
#
{
(dx/(d theta) = 2 (sin(2 theta) + sin(pi/4 + 2 theta))),
(dy/(d theta)=-2 (cos(2 theta) + cos(pi/4+ 2 theta)))
:}
#
but
#(dy)/(dx) = (((dy)/(d theta)))/(((dx)/(d theta)))#
at point #theta_0 = -(5pi)/12# we have
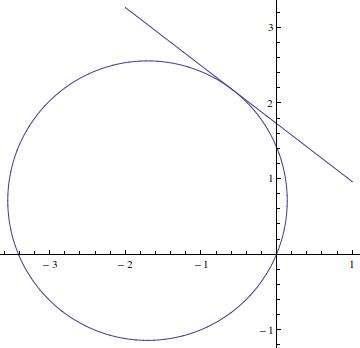
#p_0 ={r(theta_0)cos(theta_0),r(theta_0)sin(theta_0)}={-0.582262,2.17303}#
and
#m_0 = ((dy)/(dx) )_{theta_0} = -0.767327#
The tangent straight reads
#y = 2.17303 -0.767327(x+0.582262)#