The reference Tangents with Polar Coordinates gives us the equation:
#dy/dx = ((dr)/(d theta)sin(theta)+rcos(theta))/((dr)/(d theta)cos(theta)-rsin(theta))" [1]"#
Compute #(dr)/(d theta)#
#(dr)/(d theta) = -12cos(6theta-(4pi)/3)#
#(dr)/(d theta) = 12sin(6theta+pi/6)#
Substitute right sides of the equation for r and #(dr)/(d theta)# into equation [1]:
#dy/dx = ((12sin(6theta+pi/6))sin(theta)+(-2sin(6theta-(4pi)/3))cos(theta))/((12sin(6theta+pi/6))cos(theta)-(-2sin(6theta-(4pi)/3))sin(theta))#
The slope, m, of the tangent line is the above equation evaluated at #theta=(2pi)/3#
#m = ((12sin(6(2pi)/3+pi/6))sin((2pi)/3)+(-2sin(6(2pi)/3-(4pi)/3))cos((2pi)/3))/((12sin(6(2pi)/3+pi/6))cos((2pi)/3)-(-2sin(6(2pi)/3-(4pi)/3))sin((2pi)/3))#
#m~~-4#
The x coordinate, #x_1#, of the point of tangency is:
#x_1 = -2sin(6(2pi)/3-(4pi)/3)cos((2pi)/3)#
#x_1 = sqrt3/2#
The y coordinate, #y_1#, of the point of tangency is:
#y_1 = -2sin(6(2pi)/3-(4pi)/3)sin((2pi)/3)#
#y_1 = -1.5#
Using the point-slope form of the equation of a line:
#y = m(x-x_1)+y_1#
We obtain the following equation:
#y = -4(x-sqrt3/2)-1.5#
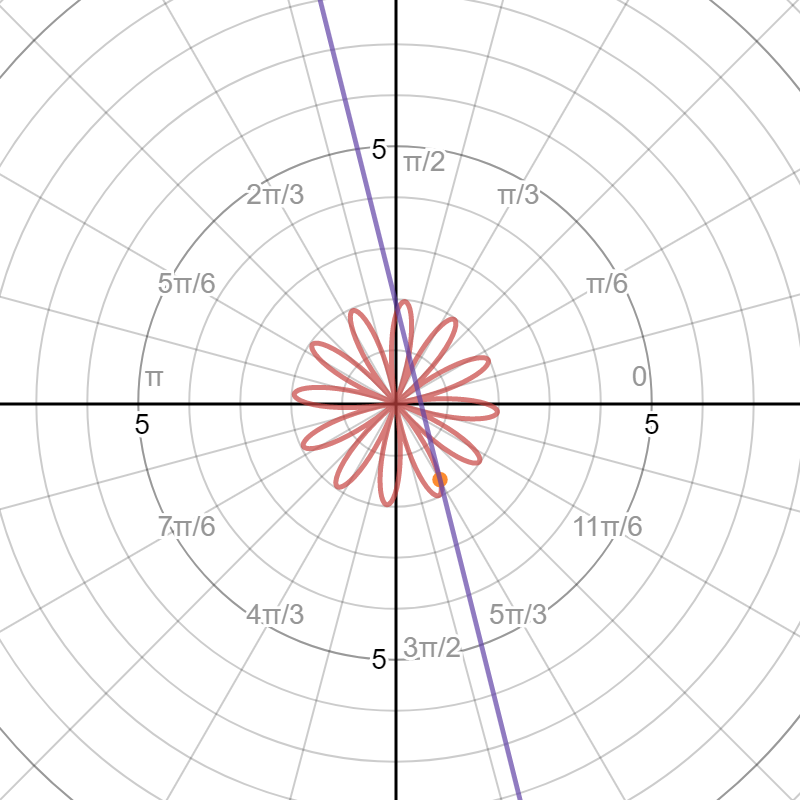
Here is a graph of the function, the point of tangency, and the tangent line: