The equation can be simplified to
#r = 1 + sin(2theta)#
using trigonometric identities.
The polar plot is shown here
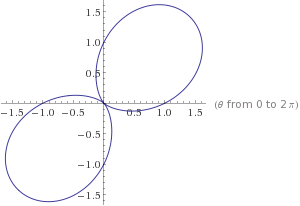
http://www.wolframalpha.com/input/?i=r%3D1%2Bsin%282theta%29
To find the tangent line, you need to know a point it passes though and its gradient, #frac{dy}{dx}#
We know that at #theta=-{3pi}/8#,
#x=rcostheta#
#= (1+sin(2(-{3pi}/8)))cos(-{3pi}/8)#
#= (2-sqrt2)^{3/2}/4#
#~~ 0.112#
#y=rsintheta#
#= (1+sin(2(-{3pi}/8)))sin(-{3pi}/8)#
#= -1/2*sqrt{{2-sqrt2}/2}#
#~~ -0.271#
The tangent line passes through #(0.112,-0.271)#.
We also know that at #theta=-{3pi}/8#,
#frac{dx}{d theta} = frac{d}{d theta}(r sintheta)#
#= frac{d}{d theta}((1+sin(2theta))*cos(theta))#
#= frac{-2sin(theta)+cos(theta)+3cos(3theta)}{2}#
Substituting #theta=-{3pi}/8#, we have
#frac{dx}{d theta}_{theta=-{3pi}/8} = -1/2*sqrt{{2-sqrt2}/2}#
#~~ -0.271#
Similarly,
#frac{dy}{d theta} = frac{d}{d theta}(r sintheta)#
#= frac{d}{d theta}((1+sin(2theta))*sin(theta))#
#= 2sin(theta)cos(2theta) + (sin(2theta)+1)*cos(theta)#
Substituting #theta=-{3pi}/8#, we have
#frac{dy}{d theta}_{theta=-{3pi}/8} = 1/2*sqrt{frac{26-7sqrt{2}}{2}}#
#~~ 1.42#
From the chain rule, we can calculate the gradient as
#frac{dy}{dx} = frac{ frac{dy}{d theta} }{ frac{dx}{d theta} }#
#= -sqrt{19+6sqrt{2}}#
#~~ 5.24#
Equation of tangent line:
#frac{y-(-1/2*sqrt{{2-sqrt2}/2})}{x-(2-sqrt2)^{3/2}/4}=-sqrt{19+6sqrt{2}}#

