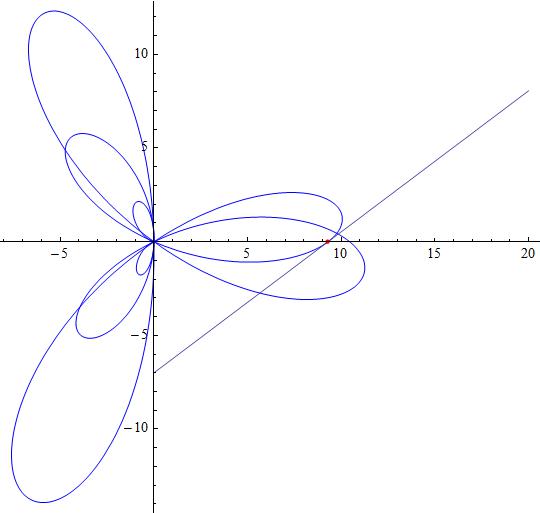
What is the equation of the tangent line to the polar curve # f(theta)=theta^2cos(3theta)-thetasin(2theta)+tan(theta/6) # at #theta = pi#?
1 Answer
Jun 14, 2016
Explanation:
The pass equations are
The tangent space is obtained making
but
with
Deriving and calculating for
so the tangent line at