Question

What is the length of a diagonal of a square if its area is 98 square feet?

Answer 1

`" "`
Length of the diagonal is `color(blue)(14` feet (approximately)

Explanation:

`" "`
Given:

A square `ABCD` with area of `color(red)(98` square feet.

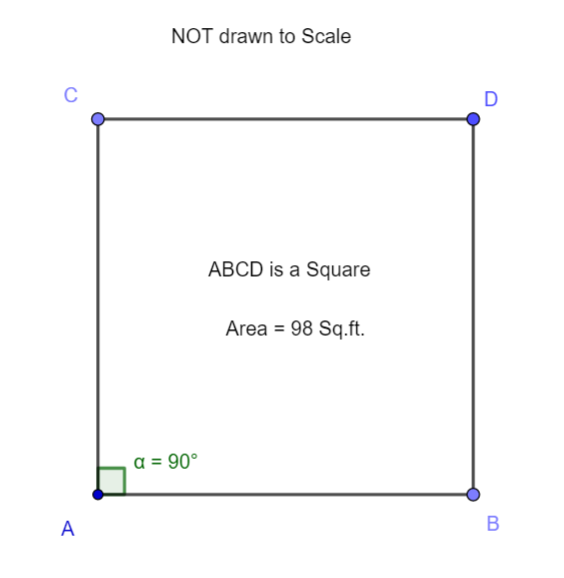
What do we need to find?

We need to find the length of the diagonal.

Properties of a Square:

1. All the magnitudes of sides of a square are congruent.

2. All the four internal angles are congruent, angle = `90^@`

3. When we draw a diagonal, as is shown below, we will have a right triangle, with the diagonal being the hypotenuse.

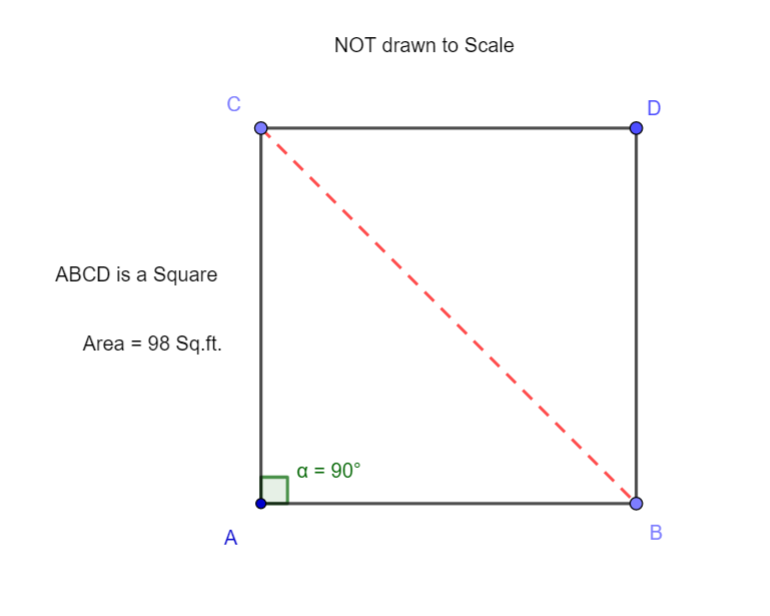
Observe that `BAC` is a right triangle, with the diagonal `BC` being the hypotenuse of the right triangle.

`color(green)("Step 1":`

We are given the area of the square.

We can find the side of the square, using the area formula.

Area of a square: `color(blue)("Area = " "(Side)"^2`

`rArr "(Side)^2=98`

Since all the sides have equal magnitudes, we can consider any one side for the calculation.

`rArr (AB)^2=98`

`rArr AB=sqrt(98)`

`rArr AB~~9.899494937`

`rArr AB~~9.9` units.

Since all the sides are equal,

`AB=BD=CD=AD`

Hence, we observe that

`AB~~9.9 and AC=9.9` units

`color(green)("Step 2":`

Consider the right triangle `BAC`

Pythagoras Theorem:

`(BC)^2 = (AC)^2+(AB)^2`

`(BC)^2=9.9^2 + 9.9^2`

Using the calculator,

`(BC)^2=98.01+98.01`

`(BC)^2=196.02`

`BC=sqrt(196.02`

`BC~~14.00071427`

`BC~~14.0`

Hence,

the length of the diagonal (BC) is approximately equal to `color(red)(14 " feet."`

Hope it helps.

Answer 2

14

Explanation:

The side is the square root of the area

`S xx S = A`

S = `sqrt 98`

The diagonal is the hypotheus of a right triangle formed by the two sides so

`C^2 = A^2 + B^2`

Where C = the diagonal A = `sqrt 98` , B = `sqrt 98`

so `C^2 = (sqrt 98)^2 + (sqrt 98)^2`

this gives

`C^2 = 98 + 98` or

`C^2 = 196`

`sqrt C^2 = sqrt 196`

`C = 14`

The diagonal is 14