Question

What is the maximum volume of the box, given the parameters below?

Given a rectangular sheet of cardboard, `16` in. by `10` in., you are asked to cut off identical squares from each of the four corners of the sheet and then bend up the sides of the remaining cardboard to form a rectangular box.

Answer 1

`x = 2` results in the maximum volume.

The associated max volume is given by:

`V=144` cubic inches

Explanation:

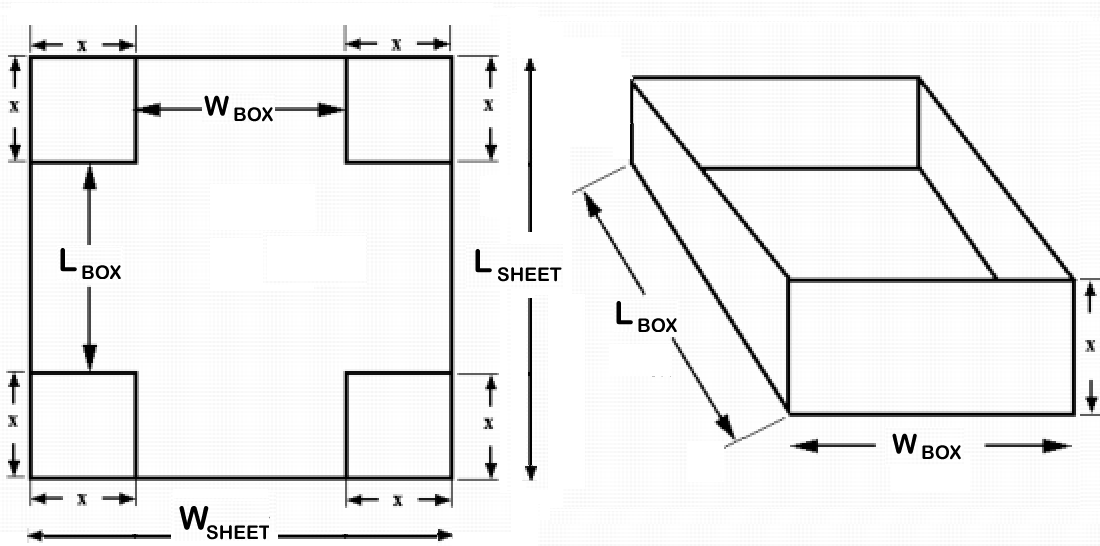
Let us set up the following variables:

`{(w, "Width of the Box (in)"), (l, "Length of the Box (in)"), (x, "Length of the Corner Cut-out (in)"), (V, "Volume of the Box (cubic in)") :}`

We want to vary the corner length `x` such that we maximise `V`, ie find a critical point of `(dV)/dx` that is a maximum, so we to find a function `V=V(x)`.

The dimensions of the sheet are 16" by 10", hence, wlog (without loss of generality) taking `w=16` we get:

Width: `x+w+x=16 \ \ => w=16-2x = 2(8-x)`
Length: `x+l+x=10 => l=10-2x = 2(5-x)`

Then the volume is given by:

`\ \ \ \ \ V=wlx`
`:. V = 2(8-x)2(5-x)x`
`:. V = 4x(x^2-13x+40)`
`:. V = 4x^3-52x^2+160x`

Differentiating wrt `x` gives us;

`:. (dV)/dx=12x^2-104x+160`

At a critical point, `(dV)/dx=0`

`:. 12x^2-104x+160 = 0`
`:. 3x^2-26x+40 = 0`
`:. (3x-20)(x-2) = 0`
`:. x=2,20/3 = 0`

We should check while value leads to a maximum volume

`:. (d^2V)/dx^2=24x-104`

`x = 2 => (d^2V)/dx^2 < 0 => max`
`x = 20/3 => (d^2V)/dx^2 > 0 => min`

So we have a maximum volume when `x=2`, the corresponding volume is:

`V = 4*8-52*4+160*2=32-208+320=144`

If we graph the Volume Function, `V(x)=4x^3-52x^2+160x` we can confirm our result:
graph{4x^3-52x^2+160x [-3, 10, -70, 160]}
Hopefully you can visually confirm the above #