What is the net area between #f(x) = e^(3-2x)-2x+1# and the x-axis over #x in [0, 3 ]#?

Question

1605 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-02T16:54:57

The area of f(x) bounded by #x=0andx=3# equal

#A=A_1+A_2=13.798(unite)^2#

show the steps
The sketch of our function is

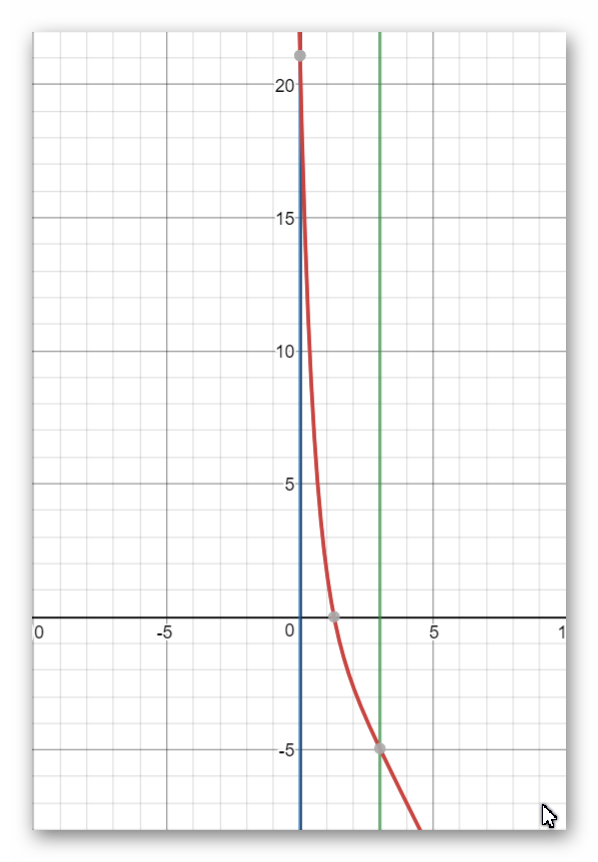
enter image source here

To find the point at which the curve intersects the axis of theX-axis

#f(x)=0#

#e^(3-2x)-2x+1=0#

#x=1.279#

#(1.279,0)#

the area equal

#A=A_1+A_2#

#A_1=int_a^bf(x)-(0)*dx#

#A_1=int_0^1.279e^(3-2x)-2x+1=[-e^(3-2*x)/2-x^2+x]_0^1.279=(9175435*e^3-20823629)/18350870=8.908019591376782(unite)^2#

#A_2=int_b^c(0)-f(x)#

#A_2=int_1.279^3(0)-(e^(3-2x)-2x+1)=[e^(3-2*x)/2+x^2-x]_1.279^3=(e^(-3)*(89281591*e^3+9175435))/18350870=4.89014466396688(unite)^2#

The area of f(x) bounded by #x=0andx=3# equal

#A=A_1+A_2=13.798(unite)^2#