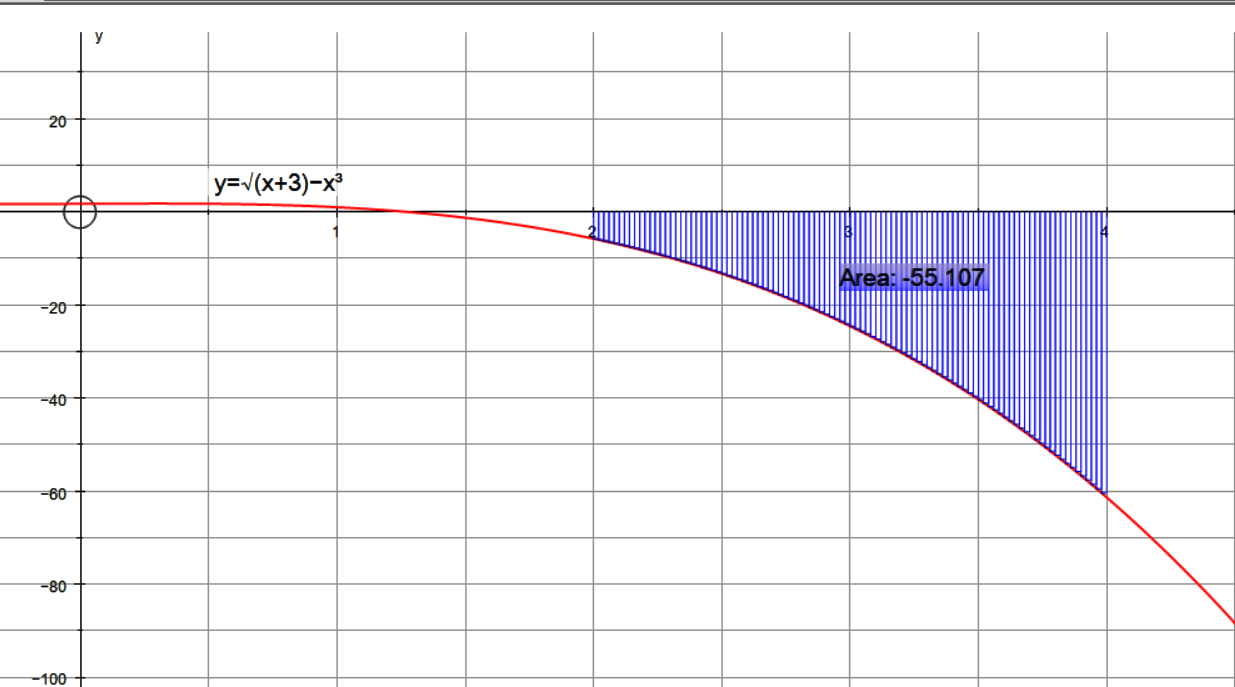
What is the net area between #f(x) = sqrt(x+3)-x^3 # and the x-axis over #x in [2, 4 ]#?

Question

1239 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-27T13:52:12

#55.107# square units ( 3 .d.p.)

Since we need the area between the x axis and the curve, in the interval #[2,4]#, our integral will be:

#int_(2)^(4)(sqrt(x+3)-x^3) dx=2/3(x+3)^(3/2)-1/4x^4#

#Area=[2/3(x+3)^(3/2)-1/4x^4]^(4)-[2/3(x+3)^(3/2)-1/4x^4]_(2)#

Plugging in upper and lowers bounds:

#Area=[2/3(4+3)^(3/2)-1/4(4)^4]^(4)-[2/3(2+3)^(3/2)-1/4(2)^4]_(2)#

#Area=[14/3sqrt(7)-64]-[10/3sqrt(5)-4]~~-55.107#

Area #= 55.107# square units.

GRAPH:

enter image source here