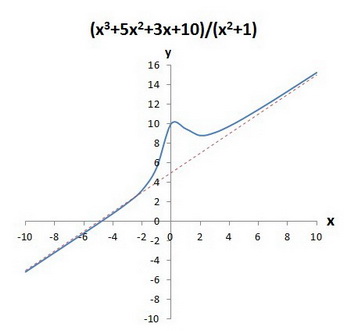
What is the oblique asymptote of #y = ( x^3 + 5x^2 + 3x + 10 )/( x^2 + 1 )#?
1 Answer
Sep 2, 2015
The oblique asymptote is
Explanation:
A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.
To find the slant asymptote you must divide the numerator by the denominator.
I will use synthetic division:
The quotient is
We can ignore the remainder, so the oblique asymptote is