What is the orbital angular momentum quantum number for the orbital 5#p#?

I don't understand anything about it. I don't know where to start.

I don't understand anything about it. I don't know where to start.
1 Answer
Explanation:
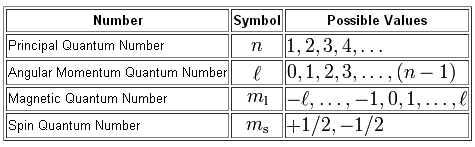 figures.boundless.com
figures.boundless.com
The first thing to note here is that you don't need to know the value of the principal quantum number,
In other words, you don't need to know the energy level on which the electron resides, which in this case would be
The
#n=5 -># this means that the electron is located on the fifth energy level
#p -># the means that it is located in the p subshell
Now, the angular momentum quantum number designates the identity of the subshell in which the electron is located
#l = 0 -># the s subshell#l=1 -># the p subshell#l=2 -># the d subshell#l=3 -># the f subshell#vdots#
In this case, the angular momentum quantum number must be equal to
As you can see from the table, for
By comparison, for
#n = 5 implies l = {0, 1, 2, 3,4 }#
The fifth energy level holds

