The best place to start is to plot the point on the Cartesian plane:
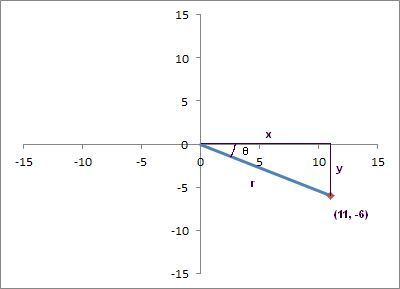
To get the polar coordinates, we need to know the distance from the origin, #r#, and the angle from the positive #x# axis, #theta#. To get these, we can simply draw the right triangle created by our point projected onto the axes. To get the distance from the origin we only need to get the hypotenuse using the Pythagorean theorem
#r^2 = x^2 + y^2#
#r=sqrt(x^2 + y^2)=sqrt(11^2 + (-6)^2) ~= 12.5#
Now we need the angle, #theta#, which can be obtained from any of #sin#, #cos#, or #tan# now that we know all the sides of our triangle
#theta = arctan(y/x) = arctan((-6)/11) ~= -28.6^o#
You'll notice that I left the negative sign in the #y# values in both cases. This ends up making the angle the correct sign. For polar form, the angle is always measured counter clockwise from the positive x-axis, so the angle in our example must be negative, since it's going clockwise from the x-axis. So the answer is
#12.5/_-28.6^o#


