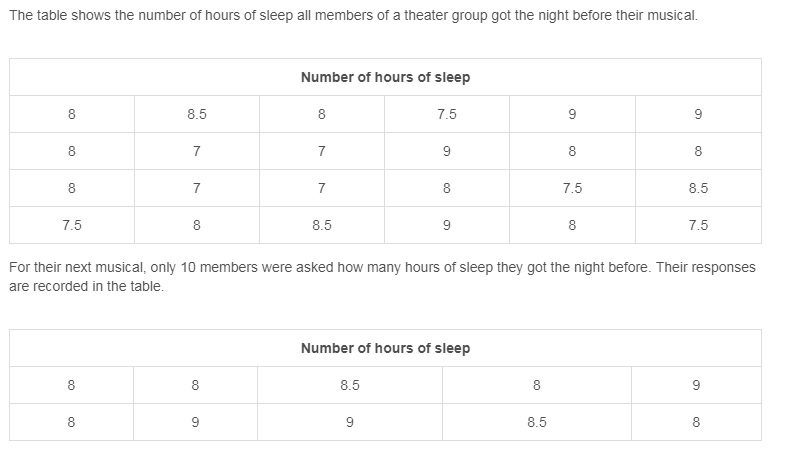
What is the sample mean for the data?
Attached screenshot: http://prntscr.com/jl73nw
Attached screenshot: http://prntscr.com/jl73nw
1 Answer
The sample mean of the last 10 data points is
Explanation:
It is unclear from the wording of the question, but since the second data set contains only 10 data points out of a possible 24, I am assuming these 10 members is what we're calling our "sample".
Under this assumption, the sample mean for these 10 data is
#barx = (8+8+8.5+8+9+8+9+9+8.5+8)/10#
#color(white)barx = 84/10#
#color(white)barx = 8.4#
Note:
While these 10 members are a sample from a population, they are not a sample from the first set of 24 data points. This is because the second set of measurements was taken on a different night, and so the hours of sleep for each member might have changed.
If we treat the
#barx = (8+8.5+8+7.5+...+9 + 8.5 + 8)/34#
#color(white)barx = 275.5/34#
#color(white)barx ~~ 8.10#
It all depends on which population we're trying to estimate the mean from.

