Question

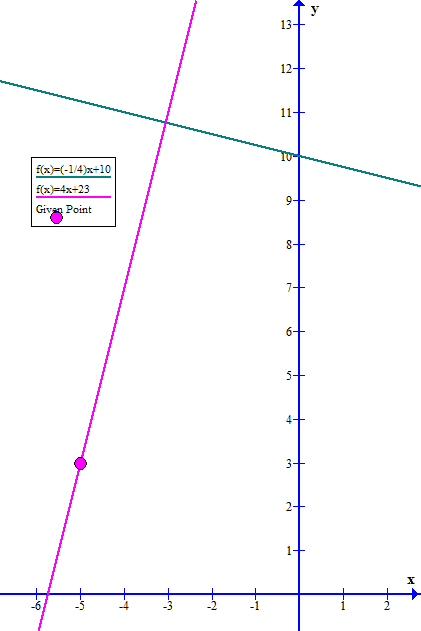
What is the slope-intercept form of equation of the line that passes through (-5, 3) and is perpendicular to `y= -1/4x+ 10`?

Answer 1

`y = 4x + 23`

Explanation:

To find the perpendicular line we first must find the slope of the perpendicular line.

The given equation is already in slope-intercept form which is:

`y = mx + c` where `m` is the slope and `c` is the y-intercept.

Therefore the slope of the line given is `-1/4`

The slope of a perpendicular line to a line with slope `a/b` is `(-b/a)`.

Converting the slope we have `(-1/4)` using this rule gives:

`-(-4/1) -> 4/1 -> 4`

Now, having the slope, we can use the point-slope formula to find the equation of the line. The point-slope formula is:

`y - y_1 = m(x - x_1)`

Where `m` is the slope, which for our problem is 4, and where (x_1, y_1) is the point, which for our problem is (-5 3).

Substituting these values gives us the formula:

`y - 3 = 4(x - -5)`

`y - 3 = 4(x + 5)`

Finally, we must solve for `y` to transform it to slope-intercept form:

`y - 3 = 4x + 20`

`y - 3 + 3 = 4x + 20 + 3`

`y - 0 = 4x + 23`

`y = 4x + 23`

Answer 2

`y=4x+23`

Explanation:

`y=color(green)(-1/4)x+10`
is the equation of a line (in slope-intercept form) with a slope of `color(green)(-1/4)`

Any line perpendicular to this line will have a slope of
`color(white)("XXX")color(magenta)(-1/(color(green)(""(-1/4)))=4`

A line through the point `(color(red)(-5),color(blue)3)` will a slope of `magenta(4)`
will have the slope-point equation:
`color(white)("XXX")y-color(blue)3=color(magenta)4(x-color(red)(""(-5)))`

`color(white)("XXX")y-3 = 4(x+5)`

Converting to slope-point form:
`color(white)("XXX")y=4x+20+3`

`color(white)("XXX")y=4x+23`