What is the slope of #2=-15y+13x#?
2 Answers
The slope is
Explanation:
To find the slope, first make the equation in slope-intercept form (shown below) so that we can find the slope easier:
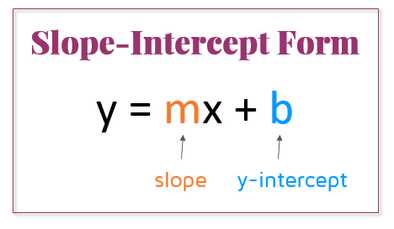
First, add
Subtract
Divide both sides by
We know that the number multiplied by
Hope this helps!
Explanation:
We can easily find the slope by converting this equation into slope-intercept form
We have the equation
Let's subtract
Next, divide both sides by
We see that the coefficient on our
Hope this helps!


